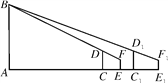
【题目】如图,学校的操场上有一旗杆AB,甲在操场上的C处竖立3 m高的竹竿CD;乙从C处退到E处恰好看到竹竿顶端D与旗杆顶端B重合,量得CE=3 m,乙的眼睛到地面的距离FE=1.5 m;丙在C1处竖立3 m高的竹竿C1D1,乙从E处后退6 m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,量得C1E1=4 m.求旗杆AB的高.
参考答案:
【答案】10.5m.
【解析】试题分析:如图,连接F1F,并延长使之与AB相交,设其与AB,CD,C1D1分别交于点G,M,N,设BG=x m,GM=y m. 根据题意分别求处DM、FG、FM、ND1、F1N、F1G的长度,根据三角形相似列方程组,解方程组即可.
试题解析:

如图,连接F1F,并延长使之与AB相交,设其与AB,CD,C1D1分别交于点G,M,N,设BG=xm,GM=ym.
∴DM=1.5m,FG=(y+3)m,FM=3m,ND1=1.5m,F1N=4m,F1G=(y+6+3)m,
∵DM∥BG,∴△FDM∽△FBG.
∴![]() =
=![]() ,则
,则![]() =
=![]() ①;
①;
又∵ND1∥GB,∴△F1D1N∽△F1BG.
∴![]() =
=![]() ,即
,即![]() =
=![]() ②;
②;
联立①②,解方程组,得![]() ,
,
故旗杆AB的高为9+1.5=10.5(m).
-
科目: 来源: 题型:
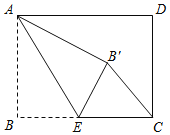
查看答案和解析>>【题目】如图,在矩形
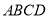 中,
中,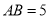 ,
,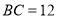 ,点
,点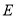 是
是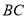 边上一点,连接
边上一点,连接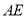 ,将
,将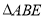 沿
沿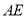 折叠,使点
折叠,使点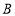 落在点
落在点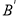 处.当
处.当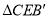 为直角三角形时,
为直角三角形时,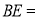 __.
__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, 为线段
为线段 上的一个动点,分别以
上的一个动点,分别以 ,
, 为边在
为边在 的同侧作菱形
的同侧作菱形 和菱形
和菱形 ,点
,点 ,
,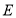 ,
, 在一条直线上,
在一条直线上, ,
, 、
、 分别是对角线
分别是对角线 ,
, 的中点,当点
的中点,当点 在线段
在线段 上移动时,线段
上移动时,线段 的最小值为________.
的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
-
科目: 来源: 题型:
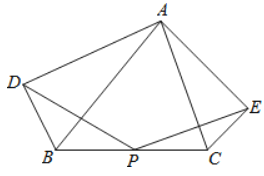
查看答案和解析>>【题目】如图,点
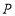 为
为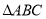 的
的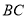 边的中点,分别以
边的中点,分别以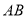 、
、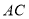 为斜边作
为斜边作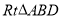 和
和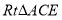 ,且
,且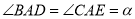 ,
,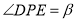 .
.
(1)求证:
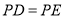 .
.(2)探究:
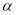 与
与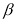 的数量关系,并证明你的结论.
的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式
直接销售
粗加工后销售
精加工后销售
每吨获利/元
100
250
450
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式
全部直接销售
全部粗加工销售
尽量精加工,剩
余部分直接销售
获利/元
(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?
(3)如果要求蔬菜都要加工后销售,且公司获利不能少于42200元,问:至少将多少吨蔬菜进行精加工?
相关试题

