【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利/元 | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工销售 | 尽量精加工,剩 余部分直接销售 |
获利/元 |
(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?
(3)如果要求蔬菜都要加工后销售,且公司获利不能少于42200元,问:至少将多少吨蔬菜进行精加工?
参考答案:
【答案】(1)14000,35000,51800(2)应安排10天进行精加工,5天进行粗加工(3)至少要将36吨蔬菜精加工
【解析】
(1)可根据获利的总额=销售方式中的销售数量×相应的销售方式对应的每吨获利的价钱.
(2)可根据精加工的加工量+粗加工的加工量=140吨.来列方程求出对应的分配时间
(3)本题的不等式关系为:精加工的获利+粗加工的获利≥42200,来列出不等式,求出自变量的取值范围,然后根据自变量的取值范围判定出符合条件的值.
解:(1)由题意得
全部直接销售的利润为:140×100=14000元;
全部粗加工后销售的利润为:140×250=35000元;
尽量精加工,剩余部分直接销售的总利润为:18×6×450+(140-18×6)×100=51800元;
故答案为:14000,35000,51800
(2)设应安排![]() 天进行精加工,
天进行精加工,![]() 天进行粗加工,根据题意得:
天进行粗加工,根据题意得:
![]()
解得![]()
所以应安排10天进行精加工,5天进行粗加工。
(3)设将![]() 吨蔬菜进行精加工,根据题意,
吨蔬菜进行精加工,根据题意,
得![]()
解得![]()
所以至少要将36吨蔬菜精加工。
-
科目: 来源: 题型:
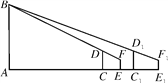
查看答案和解析>>【题目】如图,学校的操场上有一旗杆AB,甲在操场上的C处竖立3 m高的竹竿CD;乙从C处退到E处恰好看到竹竿顶端D与旗杆顶端B重合,量得CE=3 m,乙的眼睛到地面的距离FE=1.5 m;丙在C1处竖立3 m高的竹竿C1D1,乙从E处后退6 m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,量得C1E1=4 m.求旗杆AB的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
-
科目: 来源: 题型:
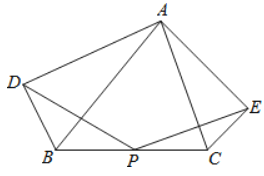
查看答案和解析>>【题目】如图,点
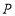 为
为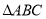 的
的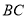 边的中点,分别以
边的中点,分别以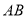 、
、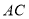 为斜边作
为斜边作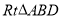 和
和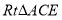 ,且
,且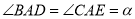 ,
,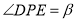 .
.
(1)求证:
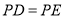 .
.(2)探究:
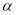 与
与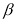 的数量关系,并证明你的结论.
的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里:
1,﹣
 ,8.9,﹣7,
,8.9,﹣7,  ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9. 正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
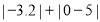 -
-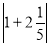 ;
;(2)0

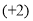



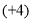

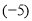
(3)(-
 )-(-
)-(-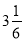 )-(+
)-(+ )+(-
)+(-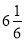 );
);(4)(- 3.125)+(+4.75)+
 +(
+(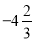 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是正方形
是正方形 对角线
对角线 上一动点,点
上一动点,点 在射线
在射线 上,且
上,且 ,连接
,连接 ,
, 为
为 中点.
中点.(1)如图1,当点
 在线段
在线段 上时,试猜想
上时,试猜想 与
与 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)如图2,当点
 在线段
在线段 上时,(1)中的猜想还成立吗?请说明理由;
上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点
 在
在 的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
相关试题

