【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】分析:根据概率的求法,找准两点:①全部情况的总数:根据题意得知这样的两位数共有90个;
②符合条件的情况数目:从总数中找出符合条件的数共有45个;二者的比值就是其发生的概率.
详解:两位数共有90个,下滑数有10、21、20、32、31、30、43、42、41、40、54、53、52、51、50、65、64、63、62、61、60、76、75、74、73、72、71、70、87、86、85、84、83、82、81、80、98、97、96、95、94、93、92、91、90共有45个,
概率为![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的半径是
的半径是 ,直线
,直线 与
与 相交于
相交于 、
、 两点.
两点. 是
是 上的一个动点,若
上的一个动点,若 ,则
,则 面积的最大值是________.
面积的最大值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是
是 的直径,
的直径, 是
是 的弦,弦
的弦,弦 于点
于点 ,交
,交 于点
于点 ,过点
,过点 的直线与
的直线与 的延长线交于点
的延长线交于点 ,
, .
.
 求证:
求证: 是
是 的切线;
的切线; 当点
当点 在劣弧
在劣弧 上运动时,其他条件不变,若
上运动时,其他条件不变,若 .求证:点
.求证:点 是
是 的中点;
的中点; 在满足
在满足 的条件下,
的条件下, ,
, ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,AC=AE,BC=DE,点E在BC上.

(1)求证:△ABC≌△ADE;(2)求证:∠EAC=∠DEB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )

A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是( )

A.
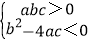 B.
B. 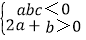 C.
C.  D.
D. 
相关试题

