【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
参考答案:
【答案】4 30
【解析】
首先求得正六边形围成的多边形的内角的度数,然后根据多边形的内角和定理即可求得n的值.
正八边形的内角度数是:![]() =135°,
=135°,
则正八边形围成的多边形的内角的度数是:360°-2×135°=90°,
根据题意得:180(n-2)=90n,
解得:n=4.
若边长为1的正n边形作环状连接,中间围成的是等边三角形,
则一个公共点处组成的角度为360°-60°=300°,
所以正n边形的一个内角是150°,
所以(n-2)×180=150n,
解得n=12,
所以边长为1的正十二边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为30.
故答案为:4,30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境
在
 中,
中, ,
, ,
, 于点
于点 ,点
,点 是射线
是射线 上一点,连接
上一点,连接 ,过点
,过点 作
作 于点
于点 ,且交直线
,且交直线 于点
于点 .
.


(1)如图1,当点
 在线段
在线段 上时,求证:
上时,求证: .
. 自主探究
(2)如图2,当点
 在线段
在线段 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.拓展延伸
(3)如图3,当点
 在线段
在线段 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出 与
与 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的半径是
的半径是 ,直线
,直线 与
与 相交于
相交于 、
、 两点.
两点. 是
是 上的一个动点,若
上的一个动点,若 ,则
,则 面积的最大值是________.
面积的最大值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是
是 的直径,
的直径, 是
是 的弦,弦
的弦,弦 于点
于点 ,交
,交 于点
于点 ,过点
,过点 的直线与
的直线与 的延长线交于点
的延长线交于点 ,
, .
.
 求证:
求证: 是
是 的切线;
的切线; 当点
当点 在劣弧
在劣弧 上运动时,其他条件不变,若
上运动时,其他条件不变,若 .求证:点
.求证:点 是
是 的中点;
的中点; 在满足
在满足 的条件下,
的条件下, ,
, ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A.
 B.
B.  C.
C. 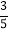 D.
D. 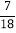
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,AC=AE,BC=DE,点E在BC上.

(1)求证:△ABC≌△ADE;(2)求证:∠EAC=∠DEB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )

A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
相关试题

