【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
利用抛物线开口方向得到a>0,利用抛物线的对称轴在直线x=1的右侧得到b<0,b<-2a,即b+2a<0,利用抛物线与y轴交点在x轴下方得到c<0,也可判断abc>0,利用抛物线与x轴有2个交点可判断b2-4ac>0,利用x=1可判断a+b+c<0,利用上述结论可对各选项进行判断.
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在直线x=1的右侧,
∴x=-![]() >1,
>1,
∴b<0,b<-2a,即b+2a<0,
∵抛物线与y轴交点在x轴下方,
∴c<0,
∴abc>0,
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,
∵x=1时,y<0,
∴a+b+c<0.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A.
 B.
B.  C.
C. 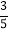 D.
D. 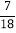
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,AC=AE,BC=DE,点E在BC上.

(1)求证:△ABC≌△ADE;(2)求证:∠EAC=∠DEB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )

A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
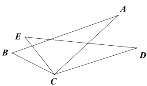
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
相关试题

