【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.
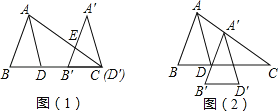
(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
参考答案:
【答案】(1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=![]() ∠BAC,即可得出∠B′A′D′=
∠BAC,即可得出∠B′A′D′=![]() ∠B′A′C.
∠B′A′C.
解:(1)∠B′EC=2∠A′,
理由:∵将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=![]() ∠BAC=
∠BAC=![]() ∠B′EC,
∠B′EC,
即∠B′EC=2∠A′;
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移至如图(2)所示,得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C,
∵∠BAD=![]() ∠BAC,
∠BAC,
∴∠B′A′D′=![]() ∠B′A′C,
∠B′A′C,
∴A′D′平分∠B′A′C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(4分)2016年在东安县举办了永州市首届中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分;负一场积0分.某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是______________场.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
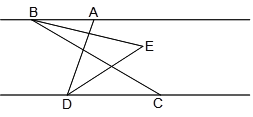
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法:

①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有 (只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.

(1)求证:DC//AB.
(2)求∠AFE的大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
 (2)
(2)
(3)(2x-1)(x-3) (4)

(5)
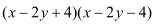
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ax2+bx+1与3x+1的积不含x3的项,也不含x的项,那么a=________,b=_________.
相关试题

