【题目】(4分)2016年在东安县举办了永州市首届中学生足球比赛,比赛规则是:胜一场积3分,平一场积1分;负一场积0分.某校足球队共比赛11场,以负1场的成绩夺得了冠军,已知该校足球队最后的积分不少于25分,则该校足球队获胜的场次最少是______________场.
参考答案:
【答案】8
【解析】设获胜的场数是x场,则平了(11-1-x)场,由题意得
3x+(11-1-x) ≥25
解之得
x≥7.5
∴该校足球队获胜的场次最少是8场.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是( )
A. ∠A B. ∠B C. ∠C D. ∠B或∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个三角形ABC中,∠A=∠B=45°,则△ABC是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,0,2,﹣3这四个数中,最小的数是( )
A.2
B.0
C.﹣2
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
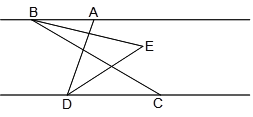
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法:

①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有 (只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.
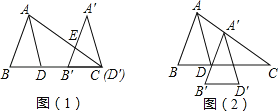
(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
相关试题

