【题目】如图,OA⊥OB,AB⊥x轴于C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.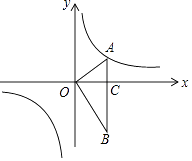
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
参考答案:
【答案】
(1)
解:把A( ![]() ,1)代入反比例函数y=
,1)代入反比例函数y= ![]() 得:k=1×
得:k=1× ![]() =
= ![]() ,
,
所以反比例函数的表达式为y= ![]() ;
;
(2)
解:∵A( ![]() ,1),OA⊥AB,AB⊥x轴于C,
,1),OA⊥AB,AB⊥x轴于C,
∴OC= ![]() ,AC=1,
,AC=1,
OA= ![]() =
= ![]() =2,
=2,
∵tanA= ![]() =
= ![]() ,
,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC﹣2 ![]() ,
,
∴S△AOB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵S△AOP= ![]() S△AOB,
S△AOB,
∴ ![]() ,
,
∵AC=1,
∴OP=2 ![]() ,
,
∴点P的坐标为(﹣2 ![]() ,0).
,0).
【解析】(1)把A的坐标代入反比例函数的解析式,即可求出答案;(2)求出∠A=60°,∠B=30°,求出线段OA和OB,求出△AOB的面积,根据已知S△AOP= ![]() S△AOB , 求出OP长,即可求出答案.
S△AOB , 求出OP长,即可求出答案.
【考点精析】关于本题考查的比例系数k的几何意义,需要了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子元件厂准备生产1200个电子元件,生产一半后,由于要尽快投入市场,该厂提高了生产效率,每天生产的电子元件个数是原来的1.2倍,结果提前2天完成了任务,求该厂后来每天生产电子元件多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解下列方程:
(1)x-1=3;
(2)-5x=15;
(3)5x+4=-24;
(4)0.2x-0.5=0.7;
(5)2x-1=4x+3;
(6)4-3x=2x-1.
-
科目: 来源: 题型:
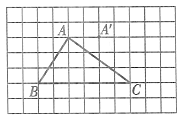
查看答案和解析>>【题目】(1)如图,平移三角形ABC,使点A平移到点
 ,画出平移后的三角形
,画出平移后的三角形 ;
;(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.
-
科目: 来源: 题型:
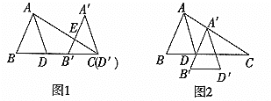
查看答案和解析>>【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形△A'B'D',A'B'交AC于点E,AD平分∠BAC.
(1)猜想∠B'EC与∠A'之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到△A'B'D',请问:A'D'平分∠B'A'C吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】联想与探索:
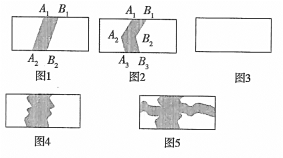
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
相关试题

