【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
参考答案:
【答案】(1)y=﹣(x﹣2)2+1;(2)见解析
【解析】
试题分析:(1)先将点(﹣1,﹣8),(0,﹣3)代入y=﹣x2+bx+c,列出关于b、c的二元一次方程组,求解得出b、c的值,得到二次函数的表达式,再用配方法化为顶点式的形式
(2)利用描点法画出函数图象即可.
解:(1)∵二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3),
∴![]() ,解得
,解得![]() ,
,
∴此二次函数的表达式为y=﹣x2+4x﹣3;
y=﹣x2+4x﹣3=﹣(x﹣2)2+1;
(2)∵y=﹣(x﹣2)2+1,
∴顶点坐标为(2,1),对称轴方程为x=2.
∵函数二次函数y=﹣x2+4x﹣3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省舟山市第7题)一元二次方程2x2﹣3x+1=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,反比例函数y=
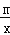 的图象过点A(1,6).
的图象过点A(1,6).(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数y=
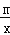 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
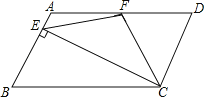
(1)若∠CFD=55°,求∠BCD的度数;
(2)求证:∠EFC=2∠CFD;
(3)求证:CE⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学课上,老师要求学生根据图示张鑫与李亮的对话内容,展开如下活动:
活动1:仔细阅读对话内容

活动2:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,她需要付多少钱?
(2)你认为买多少元钱的书办卡就便宜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).

解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在争创全国卫生城市的活动中,某市“青年突击队’决定义务清运一堆重达100吨的垃圾,在清运了25吨后,由于周围居民的加入,使清运的速度比原来提高了一倍,结果仅用了5小时就完成了本次清运工作,青年突击队原来每小时清运多少吨垃圾?
相关试题

