【题目】如图, ![]() 是⊙O外一点,
是⊙O外一点, ![]() 为切线,割线
为切线,割线 ![]() 经过圆心
经过圆心 ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的半径长;
的半径长;
(2)作 ![]() 的角平分线交
的角平分线交 ![]() 于
于 ![]() ,求
,求 ![]() 的度数.
的度数.
参考答案:
【答案】
(1)解:连接OC,∵PC是⊙O的切线,∴∠PCO=90°,设⊙O的半径长为r,在Rt△PCO中,PC= ![]() ,PO=12-r,CO=r,由勾股定理得:
,PO=12-r,CO=r,由勾股定理得: ![]() ,解得r=4;
,解得r=4;

(2)解:∵DP是∠BPC的角平分线,
∴∠CPB=2∠BPD,
∵OC=OB,
∴∠COP=2∠OBC=2∠OCB,在△PCB中,∠CPB+∠B+PCB=180°,
∵∠PCO=90°,
∴∠CPO+∠COP=45°,
∴∠DPB+∠B=45°,
∴∠CDP=∠DPB+∠B=45°.
【解析】【(1)由已知PC是⊙O的切线,添加辅助线连接OC,在Rt△PCO中,利用勾股定理,建立方程即可求出圆的半径。
(2)根据角平分线的定义得出∠CPB=2∠BPD,再根据等腰三角形的性质及三角形的外角的性质证出∠COP=2∠OBC=2∠OCB,然后根据三角形的内角和定理及等量代换即可求得结果。
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),C(﹣1,2),且
 .
.(1)求a,b的值;
(2)y轴上是否存在一点M,使△COM的面积是△ABC的面积的一半,求点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB上任意一点,PF⊥AC于F,PE⊥BC于E,则EF的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商城销售
 、
、 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为 元、
元、 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:销售时段
销售型号
销售收入
 种型号
种型号 种型号
种型号第一周
 台
台 台
台 元
元第二周
 台
台 台
台 元
元(1)求
 、
、 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;(2)若商城准备用不多于
 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共 台,求
台,求 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?(3)在(2)的条件下商城销售完这
 台电风能否实现利润超过
台电风能否实现利润超过 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进价).经过若干年销售得知,年销售量
 (万件)是销售单价
(万件)是销售单价  (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:销售单价
 (元)
(元)16
18[
20[
22
年销售量
 (万件)
(万件)5
4
3
2
(1)则 关于
关于  的函数关系式是;
的函数关系式是;
(2)写出该公司销售这种产品的年利润 (万元)关于销售单价
(万元)关于销售单价  (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价  为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于14万元(请直接写出销售单价 的范围).
的范围). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,矩形
中,矩形  的边
的边 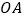 在
在  轴上,顶点
轴上,顶点 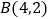 在抛物线
在抛物线  上,且抛物线交
上,且抛物线交  轴于另一点
轴于另一点  .
.
(1)则 = ,
= ,  =;
=;
(2)已知 为
为  边上一个动点(不与
边上一个动点(不与  、
、  重合),连结
重合),连结 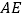 交
交  于点
于点  ,过点
,过点  作
作 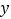 轴的平行线分别交抛物线、直线
轴的平行线分别交抛物线、直线  于
于  、
、 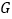 .
.
①求线段 的最大值,此时
的最大值,此时 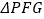 的面积为;
的面积为;
②若以点 为圆心,
为圆心,  为半径作⊙O,试判断直线
为半径作⊙O,试判断直线 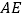 与⊙O的能否相切,若能请求出
与⊙O的能否相切,若能请求出  点坐标,若不能请说明理由.
点坐标,若不能请说明理由.
相关试题

