【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进价).经过若干年销售得知,年销售量 ![]() (万件)是销售单价
(万件)是销售单价 ![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 16 | 18[ | 20[ | 22 |
年销售量 | 5 | 4 | 3 | 2 |
(1)则 ![]() 关于
关于 ![]() 的函数关系式是;
的函数关系式是;
(2)写出该公司销售这种产品的年利润 ![]() (万元)关于销售单价
(万元)关于销售单价 ![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价 ![]() 为何值时,年利润最大?
为何值时,年利润最大?
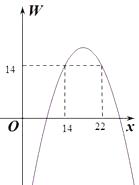
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于14万元(请直接写出销售单价 ![]() 的范围).
的范围).
参考答案:
【答案】
(1)解:设y=kx+b,把(16,5),(18,4)代入得: ![]() ,解得:
,解得: 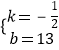 ,故答案为
,故答案为 ![]() ;
;
(2)解:该公司年利润w=(x-10)( ![]() )-10=
)-10= ![]() ,当x=18时,该公司年利润最大值为22万元;
,当x=18时,该公司年利润最大值为22万元;
(3)解:由题意得 ![]() =14,解得
=14,解得 ![]() ,
, ![]() ,故该公司确定销售单价x的范围是:14≤x≤22.
,故该公司确定销售单价x的范围是:14≤x≤22.
【解析】(1)抓住已知年销售量 y (万件)是销售单价 x (元)的一次函数,因此根据表中的已知点的坐标,利用待定系数法确定一次函数的解析式即可
(2)根据总利润=每一件的利润×销售量,列出函数关系式,化为顶点式即可确定最值。
(3)根据不等关系,年利润≥14,建立不等式,求得相应的自变量取值范围,即可解答本题。或根据函数图像求出销售单价 x 的范围。
【考点精析】利用确定一次函数的表达式和二次函数的最值对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB上任意一点,PF⊥AC于F,PE⊥BC于E,则EF的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙O外一点,
是⊙O外一点,  为切线,割线
为切线,割线  经过圆心
经过圆心  .
.
(1)若 ,求
,求  的半径长;
的半径长;
(2)作 的角平分线交
的角平分线交  于
于  ,求
,求  的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商城销售
 、
、 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为 元、
元、 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:销售时段
销售型号
销售收入
 种型号
种型号 种型号
种型号第一周
 台
台 台
台 元
元第二周
 台
台 台
台 元
元(1)求
 、
、 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;(2)若商城准备用不多于
 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共 台,求
台,求 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?(3)在(2)的条件下商城销售完这
 台电风能否实现利润超过
台电风能否实现利润超过 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,矩形
中,矩形  的边
的边 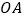 在
在  轴上,顶点
轴上,顶点 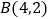 在抛物线
在抛物线  上,且抛物线交
上,且抛物线交  轴于另一点
轴于另一点  .
.
(1)则 = ,
= ,  =;
=;
(2)已知 为
为  边上一个动点(不与
边上一个动点(不与  、
、  重合),连结
重合),连结 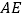 交
交  于点
于点  ,过点
,过点  作
作 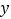 轴的平行线分别交抛物线、直线
轴的平行线分别交抛物线、直线  于
于  、
、 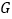 .
.
①求线段 的最大值,此时
的最大值,此时 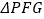 的面积为;
的面积为;
②若以点 为圆心,
为圆心,  为半径作⊙O,试判断直线
为半径作⊙O,试判断直线 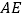 与⊙O的能否相切,若能请求出
与⊙O的能否相切,若能请求出  点坐标,若不能请说明理由.
点坐标,若不能请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(1)-32+(-
 )-2-(π-5)0-|-2|;
)-2-(π-5)0-|-2|;(2)
 ;
;(3)
 ;
;(4) (2m+3)(2m-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

相关试题

