Question

【题目】如图，在平面直角坐标系中，已知A（a，0），B（b，0），C（﹣1，2），且．

（1）求a，b的值；

（2）y轴上是否存在一点M，使△COM的面积是△ABC的面积的一半，求点M的坐标．

Answer 1

【答案】（1）a=－2，b=3；（2）M(0，－5)或M(0，5)．

【解析】

（1）根据非负数的性质列出关于a、b的二元一次方程组，然后解方程组即可；

（2）过点C作CT⊥x轴，CS⊥y轴，垂足分别为T、S，根据点A、B的坐标求出AB，再根据点C的坐标求出CT、CS，然后根据三角形的面积求出OM，再写出点M的坐标即可．

（1）∵，

又∵|2a＋b＋1|≥0，（a＋2b4）2≥0，

∴|2a＋b＋1|＝0且（a＋2b4）2＝0，

∴，

解得，

即a＝2，b＝3；

（2）过点C作CT⊥x轴，CS⊥y轴，垂足分别为T、S．

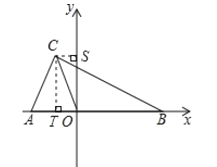
∵A（2，0），B（3，0），

∴AB＝5，

∵C（1，2），

∴CT＝2，CS＝1，

∵△ABC的面积＝ABCT＝5，

∴要使△COM的面积＝△ABC的面积，

则△COM的面积＝，

即OMCS＝，

∴OM＝5，

所以M的坐标为（0，5）或(0，-5)．