【题目】在平面直角坐标系中,我们定义点P(a ,b )的“伴随点”为Q,且规定:当a ≥ b时,Q为( b,-a );当 a<b 时,Q为( a,-b).
(1)点(2,1)的伴随点坐标为__________;
(2)若点A(a ,2)的伴随点在函数y=![]() 的图像上,求a的值;
的图像上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的伴随点组成一个新的图形记作M.请直接写出直线y=—x+c与图形M有交点时相应的c的取值范围为__________.
参考答案:
【答案】 (1,—2) c≤0
【解析】(1)根据“伴随点”的定义直接写出答案即可;(2)分两种情况求a的值即可;(3)先求得直线l的解析式,再求得当x与y值相等时点C的坐标,根据“伴随点”的定义求得新的图形M是以![]() 为端点的两条射线组成的图形,再确定c的取值范围即可.
为端点的两条射线组成的图形,再确定c的取值范围即可.
(1)(1,—2);
(2)当a≥2时,“伴随点”为(2,—a),则—2 a=1,a=![]() (舍);
(舍);
当a<2时,“伴随点”为(a,—2),则a=![]() ;
;
(3)设直线l的解析式为y=kx+b,将点(6,0)、(0,3)代入y=kx+b,得:
![]() ,
,
解得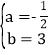 ,
,
∴直线l的解析式为![]()
当x=y时,![]() ,解得x=2;
,解得x=2;
点C的坐标为(2,-2),点C的“伴随点”的坐标为![]() ,
,
点(6,0)的“伴随点”的坐标为(0,-6),点(0,3)的“伴随点”的坐标为(0,-3),
当x≥2时,所有“伴随点”组成的图形是以![]() 为端点,过(0,-6)的一条射线;即:y=2x-6,其中x≥2;
为端点,过(0,-6)的一条射线;即:y=2x-6,其中x≥2;
当x<2时,所有变换点“伴随点”组成的图形是以![]() 为端点,过(0,-3)的一条射线,即
为端点,过(0,-3)的一条射线,即![]() ,其中,x<2;
,其中,x<2;
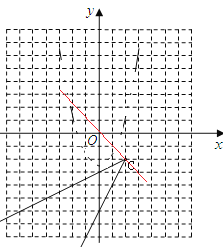
所以新的图形M是以![]() 为端点的两条射线组成的图形(如图).
为端点的两条射线组成的图形(如图).
因直线y=—x+c与图形M有交点,把![]() 代入y=—x+c可求得c=0,
代入y=—x+c可求得c=0,
∴直线y=—x+c与图形M有交点时c的取值范围为:c≤0.
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
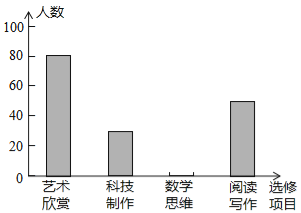
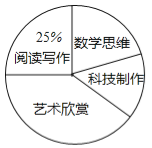
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
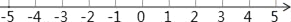
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
相关试题

