【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
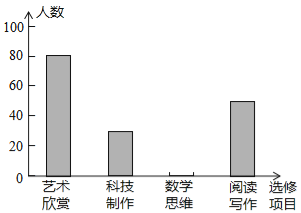
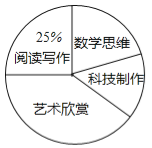
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
参考答案:
【答案】解:(1)200,144。
(2)补图如下:
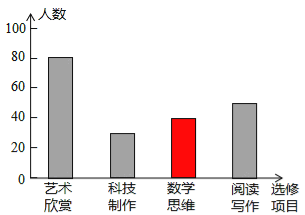
(3)120名
【解析】
(1)根据阅读写作的人数和所占的百分比,即可求出总学生数:50÷25%=200(名);再用艺术鉴赏的人数除以总人数乘以360°,即可得出 “艺术鉴赏”部分的圆心角是![]() ×360°=144°。
×360°=144°。
(2)用总学生数减去“艺术鉴赏”,“科技制作”,“阅读写作”,得出“数学思维”的人数,从而补全统计图。
(3)用“科技制作”所占的百分比乘以总人数8000,即可得出答案。
解:(1)200,144。
(2)数学思维的人数是:200-80-30-50=40(名),
补图如下:

(3)根据题意得:800×![]() =120(名),
=120(名),
答:其中有120名学生选修“科技制作”项目。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上,顶点B 在第一象限,OA//CB.
(1)如图 1,若点 A(6,0),B(4,3),点 M 是 y 轴上一点,且 SBCM SAOM ,求点 M的坐标;
(2)如图 2,点 P 是 x 轴上点 A 左边的一点,连接 PB,∠PBC 和∠PAB 的角平分线交于点D,求证:∠ABP+2∠ADB=180°;
(3)如图 3,点 P 是 x 轴上点 A 左边的一点,点 Q 是射线 BC 上一点,连接 PB、PQ,∠ABP和∠BQP 的平分线相交于点 E,求
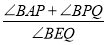 的值.
的值.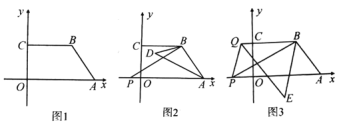
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形内一点,若S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,则S四边形DHOG= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图,E点为DF上的点,B为AC上的点,
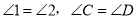 ,那么
,那么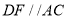 ,请完成它成立的理由
,请完成它成立的理由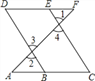
解:
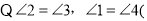 ______
______ 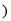
又
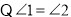
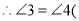 ______
______ 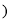
 ______
______ 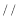 ______
______ 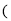 ______
______ 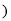
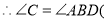 ______
______ 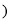
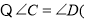 ______
______ 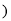
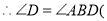 ______
______ 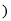
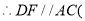 ______
______ 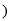
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我校七年级
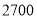 名学生的体重情况,现从中随机抽取
名学生的体重情况,现从中随机抽取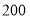 名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )
名学生测量体重进行统计分析,关于本次调查下列说法正确的是( )A.本次调查中的总体是七年级
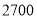 名学生
名学生B.本次调查中的样本是随机抽取的
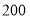 名学生的体重
名学生的体重C.本次调查中的样本容量是
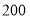 名
名D.本次调查中的个体是七年级的每个学生
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
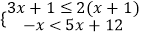 ,并写出它的整数解.
,并写出它的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:项目类型
频数
频率
跳长绳
25
a
踢毽子
20
0.2
背夹球
b
0.4
拔河
15
0.15
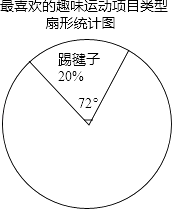
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
相关试题

