【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,这种台灯的售价每上涨1元,其销量就减少10个,
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)当售价定为多少元时,其销售利润达到最大,最大利润是多少?
参考答案:
【答案】(1)50或80; (2) 售价为65元时利润最大,利润最大为12250元;
【解析】
(1) 假设这种台灯上涨x元,根据题意列出方程![]() ,再求解即可得到答案;
,再求解即可得到答案;
(2)根据利润=每个台灯的利润×销售量列出一元二次方程,再根据二次函数的性质求最大利润即可得到答案;
解:(1) 假设这种台灯上涨x元,根据题意可得方程:
![]() ,
,
即:![]() ,
,
化简得:![]() ,
,
即:![]()
解得:![]() 或
或![]() ,
,
此时售价定价为:10+40=50(元)或者40+40=80(元);
(2)设台灯售价为x元,利润为y元,根据题意得:
![]() ,
,
即:![]() ,
,
化简得:![]()
即:![]() ,
,
根据二次函数的性质,开口向下,越靠近对称轴的点对应的值越大,对称轴处取得最大值,
因此,当x=65时,取得最大利润y=12250;
故售价为65元时利润最大为12250元;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.
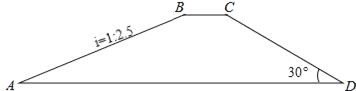
(1)求坝底AD的长度(结果精确到1米);
(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据:
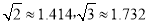 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E是边BC的中点,DE的延长线与AB的延长线相交于点F.
(1)求证:△CDE≌△BFE;
(2)试连接BD、CF,判断四边形CDBF的形状,并证明你的结论

-
科目: 来源: 题型:
查看答案和解析>>【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表如下:

零花钱数额(元)
5
10
15
20
学生个数(个)
a
15
20
5
请根据表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的众数、中位数和平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数。例如:M{1,0,2}=
 ;min{1,0,2}=1;min{1,0,a}=
;min{1,0,2}=1;min{1,0,a}= .如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
.如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )A.
 B.
B. C.1D.
C.1D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径。点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标可以表示为_____.
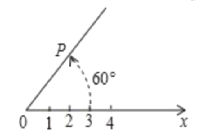
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中,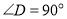 ,
,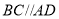 .
. ,
,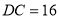 ,
,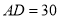 ,动点P从点D出发,沿射线
,动点P从点D出发,沿射线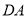 的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段
的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段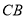 上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)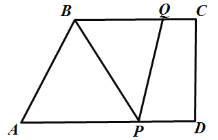
(1)设
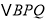 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;(2)若四边形
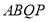 为平行四边形,求运动时间t;
为平行四边形,求运动时间t;(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?
相关试题

