【题目】在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

参考答案:
【答案】(1)、证明过程见解析;(2)、2![]()
【解析】
试题分析:(1)、根据平行四边形的性质得出∠ADF=∠CED,∠B+∠C=180°,结合∠AFE+∠AFD=180°,∠AFE=∠B,得出∠AFD=∠C,从而得出三角形相似;(2)、根据勾股定理得出DE的长度,然后根据△ADF和△DEC相似得出答案.
试题解析:(1)、∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD, ∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,∴∠AFD=∠C, ∴△ADF∽△DEC;
(2)、∵CD=AB=4,AE⊥BC,∴AE⊥AD; 在Rt△ADE中,DE=![]() ,
,
∵△ADF∽△DEC,∴![]() ; ∴
; ∴![]() ,解得AF=
,解得AF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2-kx+9能用公式法分解因式,则k的值为( )
A. ±3 B. 3 C. ±6 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
(1)求证:△BEC≌△CDB;
(2)若∠A=70°,BE⊥AC,求∠BCD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,M、N是过点A的一条直线,作 BD⊥MN于点D,CE⊥MN于点E。

(1)求证:DE=BD+CE;
(2)当直线MN绕点A旋转到图2所示的位置,其他条件不变,则BD与DE、CE的关系如何?请予以证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】若A,B,C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x-1)=2(x-1)
-
科目: 来源: 题型:
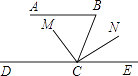
查看答案和解析>>【题目】“小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
相关试题

