【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,M、N是过点A的一条直线,作 BD⊥MN于点D,CE⊥MN于点E。

(1)求证:DE=BD+CE;
(2)当直线MN绕点A旋转到图2所示的位置,其他条件不变,则BD与DE、CE的关系如何?请予以证明

参考答案:
【答案】(1)证明见解析(2)BD=DE+CE
【解析】试题分析:(1)由题中条件可得Rt△ABD≌Rt△CAE,再由线段之间的关系写出最终结论即可;
(2)由HL得出Rt△ABD≌Rt△CAE,进而得出BD=AE,AD=CE,再由线段之间的转化即可得出结论:BD=DE+CE或DE=BD-CE.
试题解析:
(1)∵BD⊥直线MN,CE⊥直线MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
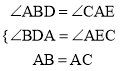
∴△ADB≌△CEA
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)关系:BD=DE+CE
证明如下:
∵BD⊥直线MN,CE⊥直线MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
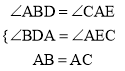
∴△ADB≌△CEA
∴AE=BD,AD=CE,
∴BD=AE=DE+AD=DE+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与﹣2距离3个单位长度的点表示的数是( )
A. 1 B. 5 C. ﹣5 D. 1和﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2-kx+9能用公式法分解因式,则k的值为( )
A. ±3 B. 3 C. ±6 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
(1)求证:△BEC≌△CDB;
(2)若∠A=70°,BE⊥AC,求∠BCD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A,B,C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(x-1)=2(x-1)
相关试题

