搜索
【题目】用配方法解方程x2+8x﹣9=0时，此方程可变形为（ ）
A.（x+4）2=7
B.（x+4）2=25
C.（x+4）2=9
D.（x+4）2=﹣7
参考答案：
【答案】B
【解析】解：x2+8x﹣9=0，
移项得：x2+8x=9，
配方得：x2+8x+16=25，即（x+4）2=25．
故选B
【考点精析】解答此题的关键在于理解配方法的相关知识，掌握左未右已先分离，二系化“1”是其次．一系折半再平方，两边同加没问题．左边分解右合并，直接开方去解题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果把电视屏幕看作一个长方形平面，建立一个直角坐标系，若左下方的点的坐标是（0，0），右下方的点的坐标是（32，0），左上方的点的坐标是（0，28），则右上方的点的坐标是_________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一列数，按一定规律排成1，﹣2，4，﹣8，16，﹣32，…，其中某三个相邻数的和是192，则这三个数中最小的数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c为正数，满足如下两个条件：
a+b+c=32 ①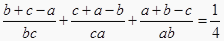
②
是否存在以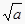
， 
， 
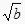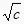为三边长的三角形？如果存在，求出三角形的最大内角． -
科目： 来源： 题型：
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．
（1）请用直尺和圆规画一个“好玩三角形”；
（2）如图1，在Rt△ABC中，∠C=90°，tanA=
，求证：△ABC是“好玩三角形”；（3）如图2，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动，记点P经过的路程为s．
①当β=45°时，若△APQ是“好玩三角形”，试求
的值；②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”．请直接写出tanβ的取值范围．
（4）依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列数字的排列规律，然后在横线上填入适当的数：3，﹣7，11，﹣15，19，﹣23， ， ， …．按照这个规律，第101个数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？
相关试题
