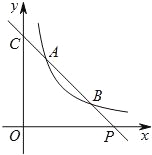
【题目】如图,已知直线y=ax+b与双曲线![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
参考答案:
【答案】(1)P点坐标为(4,0);
(2)A(2,2),B(4,1);
(3)x1+x2=x0.
【解析】
试题分析:(1)把A点坐标代入反比例函数解析式可求得k,进一步可求得B点坐标,再利用待定系数法可求得直线解析式,可求得P点坐标;
(2)过点A作AD∥x轴,交x轴于点D,利用△ACD∽△PCO,结合A、P、C的坐标可求得x1、y1之间的关系,结合AB=BP可表示出B点坐标,再结合A、B两点都在反比例函数图象上,可求得A、B两点的坐标;
(3)结合(1)、(2)中的坐标可猜得结论.
试题解析:(1)∵点A(1,3)在反比例函数y=![]() 上,∴k=3,
上,∴k=3,
∵点B(3,y2)在y=![]() 上,
上,
∴y2=1,即B点坐标为(3,1),
把A、B两点坐标代入直线y=ax+b,
可得![]() ,解得
,解得![]() ,∴直线AB的解析式为y=﹣x+4,
,∴直线AB的解析式为y=﹣x+4,
当y=0时,x=4,∴P点坐标为(4,0);
(2)如图,过A作AD∥x轴,交y轴于点D,则AD⊥y轴,
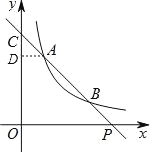
∴△ACD∽△PCO,∴![]() =
=![]() ,
,
∵b=y1+1,P(6,0),A(x1,y1),
∴CD=1,OC=y1+1,AD=x1,OP=6,
∴![]() =
=![]() ,
,
∵AB=BP,A(x1,y1),
∴B为AP中点,且P为(6,0),∴B点坐标为(![]() ,
,![]() ),∵A、B两点都在y=
),∵A、B两点都在y=![]() 上,∴x1y1=
上,∴x1y1=![]()
![]() ,解得x1=2,∴
,解得x1=2,∴![]() =
=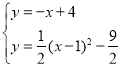 ,解得y1=2,∴A(2,2),B(4,1);
,解得y1=2,∴A(2,2),B(4,1);
(3)猜想x1,x2,x0之间的关系式为:x1+x2=x0.
理由如下:∵A(x1,y1),B(x2,y2),
∴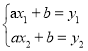 ,解得
,解得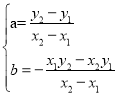 ,
,
∴直线AB解析式为y=![]() x﹣
x﹣![]() ,
,
令y=0可得x=![]() ,
,
∵x1y1=x2y2,
∴x=![]() =
=![]() =x1+x2,
=x1+x2,
即x1+x2=x0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一张宽为12cm的练习纸,相邻两条格线间的距离均为0.6cm.调皮的小段在纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上(如图),测得∠α=37°.
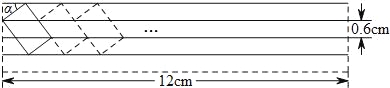
(1)求矩形图案的面积;
(2)若小段在第一个图案的右边以同样的方式继续盖印(如图),最多能印几个完整的图案?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A.3,4,8
B.5,6,11
C.1,2,3
D.5,6,10 -
科目: 来源: 题型:
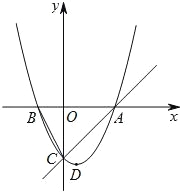
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣
 ),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.(1)求抛物线所对应的二次函数的表达式.
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围.
(3)是否存在P点,使∠PAC=∠BCO?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,直线a、b相交于O,b∥c,则a与c的位置关系是( )
A.平行
B.相交
C.重合
D.平行或重合 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式|x﹣1|<1的解集是( )
A.x>2
B.x<0
C.1<x<2
D.0<x<2 -
科目: 来源: 题型:
查看答案和解析>>【题目】按照下列步骤做一做:
(1)一个两位数的个位上的数是a,十位上的数是b,请写出这个两位数;
(2)交换这个两位数的十位数字和个位数字,得到一个新数;请写出这个新两位数;
(3)求这两个两位数的和.结果能被11整除吗?为什么?
相关试题

