【题目】现有一张宽为12cm的练习纸,相邻两条格线间的距离均为0.6cm.调皮的小段在纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上(如图),测得∠α=37°.
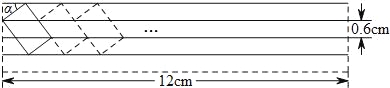
(1)求矩形图案的面积;
(2)若小段在第一个图案的右边以同样的方式继续盖印(如图),最多能印几个完整的图案?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
参考答案:
【答案】(1)1.5cm2;
(2)最多能印9个完整的图案.
【解析】
试题分析:(1)要求矩形图案的面积,只要求出矩形的长和宽即可,由题意可得分别求得矩形的长和宽,本题得以解决;
(2)要求最多能印几个完整的图案,只要求出FG、GC的长,然后用12﹣FG的差除以GC的长即可解答本题.
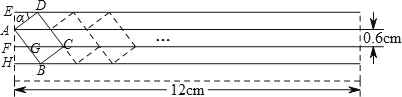
试题解析:(1)如右图所示,
∵∠α=37°,AE=0.6cm,∠ED=90°,∠DAB=90°,AH=1.2cm,
∴AD=![]() =
=![]() =1cm,∠HAB=∠α=37°,
=1cm,∠HAB=∠α=37°,
∴AB=![]() =1.5cm,
=1.5cm,
∴矩形ABCD的面积是:ADAB=1×1.5=1.5cm2,
即矩形图案的面积是1.5cm2;
(2)∵∠FAG=∠α=37°,AF=0.6cm,
∴FG=AFtan37°=0.6×0.75=0.45cm,
又∵BC=AD=1cm,∠BGC=∠FGA,∠GBC=∠GFA=90°,
∴∠GCB=∠α=37°,
∴GC=![]() =1.25cm,
=1.25cm,
∵(12﹣0.45)÷1.25=9.24,
∴最多能印9个完整的图案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3-2x2y=_________________.
-
科目: 来源: 题型:
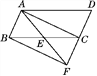
查看答案和解析>>【题目】如图,已知点E是ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
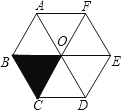
A.△OCD
B.△OAB
C.△OAF
D.△DEF -
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A.3,4,8
B.5,6,11
C.1,2,3
D.5,6,10 -
科目: 来源: 题型:
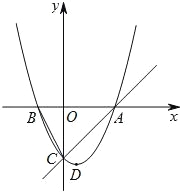
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣
 ),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.(1)求抛物线所对应的二次函数的表达式.
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围.
(3)是否存在P点,使∠PAC=∠BCO?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
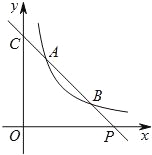
查看答案和解析>>【题目】如图,已知直线y=ax+b与双曲线
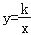 (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
相关试题

