【题目】如图,在△ABC中,BD⊥AC,垂足为D,AB=AC=9,BC=6,求BD的长. 
参考答案:
【答案】解:作AE⊥BC于E,如图所示: 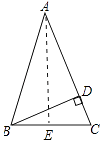
则∠AEC=90°,
∵AB=AC,
∴BE=CE= ![]() BC=3,
BC=3,
∴AE= ![]() =6
=6 ![]() ,
,
∵BD⊥AC,
∴∠BDC=90°=∠AEC,
又∵∠C=∠C,
∴△AEC∽△BDC,
∴AE:BD=AC:BC,
∴BD= ![]() =
= ![]() =4
=4 ![]() .
.
【解析】作AE⊥BC于E,由等腰三角形的性质得出BE=CE= ![]() BC=3,由勾股定理求出AE,证明△AEC∽△BDC,得出对应边成比例,即可求出BD的长.
BC=3,由勾股定理求出AE,证明△AEC∽△BDC,得出对应边成比例,即可求出BD的长.
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程、求值.
(1)解方程:x2﹣4x﹣5=0
(2)求值: sin30°+tan60°﹣cos45°+tan30°.
sin30°+tan60°﹣cos45°+tan30°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,
(1)求BF与FC的长;
(2)求EC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.

(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
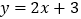 与直线
与直线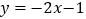 .
.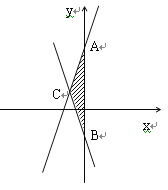
【1】(1)求两直线与
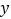 轴交点A,B的坐标;
轴交点A,B的坐标;【2】(2)求两直线交点C的坐标;
【3】(3)求△ABC的面积.
相关试题

