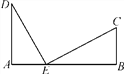
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
参考答案:
【答案】E站应建在离A站10千米处.
【解析】试题分析:根据C、D两村到E站的距离相等,可得DE=CE,在Rt△AED和Rt△EBC中,根据勾股定理可得AE2+AD2=BE2+BC2,设AE=x,则BE=25﹣x,列出方程,解方程求得x的值,即可得收购站E离A点的距离.
试题解析:
∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若4a+3b=3,求92a27b.
(2)已知3×9m×27m=321,求m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.在同一平面内,两条直线的位置只有平行和垂直两种
B.两直线平行,同旁内角相等
C.过一点有且只有一条直线与已知直线平行
D.平行于同一条直线的两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________

-
科目: 来源: 题型:
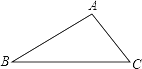
查看答案和解析>>【题目】已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2
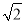 ,
, 求:(1)AB的长为________;
(2)S△ABC=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数a的平方根是2x﹣3与5﹣x,则这个正数a的值是( )
A.25B.49C.64D.81
相关试题

