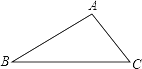
【题目】已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2![]() ,
,
求:(1)AB的长为________;
(2)S△ABC=________.
参考答案:
【答案】 4 2+2![]()
【解析】试题分析:(1)过点A作AD⊥BC,根据题意可得CD=AD,再根据勾股定理可求得AD的长,最后根据含30°的直角三角形的性质求解即可;
(2)在Rt△ABD中,得用勾股定理求得BD长,从而得到BC长,再利用三角形的面积公式计算即可得.
试题解析:(1)过点A作AD⊥BC于点D,则∠ADC=∠ADB=90°,
∵∠C=45°,∴∠DAC=90°-∠C=45°,∴∠C=∠DAC,∴AD=CD,
∵AC2=AD2+CD2,AC=![]() ,∴AD=CD=2,
,∴AD=CD=2,
∵∠ADB=90°,∠B=30°,∴AB=2AD=4,
故答案为:4;
(2)在Rt△ABD中,由勾股定理得:BD=![]() =2
=2![]() ,
,
∴BC=BD+CD=2+2![]() ,
,
∴S△ABC= ![]() =2+2
=2+2![]() ,
,
故答案为:2+2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.在同一平面内,两条直线的位置只有平行和垂直两种
B.两直线平行,同旁内角相等
C.过一点有且只有一条直线与已知直线平行
D.平行于同一条直线的两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________

-
科目: 来源: 题型:
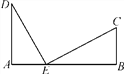
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数a的平方根是2x﹣3与5﹣x,则这个正数a的值是( )
A.25B.49C.64D.81
-
科目: 来源: 题型:
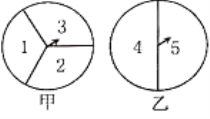
查看答案和解析>>【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
相关试题

