【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

参考答案:
【答案】(1)、证明过程见解析;(2)、平行和垂直.
【解析】试题分析:(1)、根据∠C=90°,PD⊥AB,BD为角平分线可得∠CDB=∠QEB,根据对顶角的性质可得结论;(2)、根据图示得出线段之间的关系.
试题解析:(1)、∵∠C=90° ∴∠CDB+∠CBD=90° ∵PD⊥AB ∴∠EBQ+∠QEB=90°
∵BD平分∠ABC ∴∠CBD=∠EBQ ∴∠CDB=∠QEB ∵∠QEB=∠PED ∴∠CDB=∠PED
即∠PDE=∠PED
(2)、平行和垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________

-
科目: 来源: 题型:
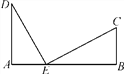
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
-
科目: 来源: 题型:
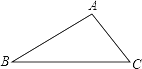
查看答案和解析>>【题目】已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2
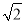 ,
, 求:(1)AB的长为________;
(2)S△ABC=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数a的平方根是2x﹣3与5﹣x,则这个正数a的值是( )
A.25B.49C.64D.81
-
科目: 来源: 题型:
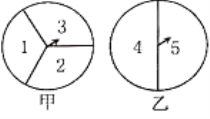
查看答案和解析>>【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,则AD是 ∠BAC的平分线吗?若是说明理由.(在下面的括号内填注依据)
解:是,理由如下:

∵AD⊥BC,EG⊥BC ( 已知 ),
∴∠4=∠5=90( 垂直的定义),
∴AD‖_____( );
∴∠1=∠E ( ),
∠2=______(两直线平行,内错角相等);
∵∠E=∠3(已知),
∴∠_____=∠____(等量代换);
∴AD平分∠BAC( ).
相关试题

