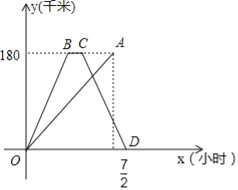
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
参考答案:
【答案】(1)慢车的速度60千米/时,快车的速度120千米/时;
(2)y=﹣120x+420(2≤x≤![]() );(3)
);(3)![]() 或
或![]() 或
或![]() 小时
小时
【解析】试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:(1)慢车的速度![]() 千米/时,
千米/时,
快车的速度=60×2=120千米/时;
(2)快车停留的时间: ![]() (小时),
(小时),
![]() (小时),即
(小时),即![]()
设CD的解析式为: ![]() 则
则
将![]() 代入,得
代入,得

解得![]() ,
,
∴快车返回过程中y(千米)与x(小时)的函数关系式为![]()
(3)相遇之前: ![]()
解得![]()
相遇之后: ![]()
解得![]()
快车从甲地到乙地需要![]() 小时,
小时,
快车返回之后: ![]()
解得![]()
综上所述,两车出发后经过![]() 或
或 ![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.0既不是整数也不是分数B.整数与分数统称为有理数
C.一个数的绝对值一定是正数D.倒数等于本身的数是1
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-3.5,小于3.9的整数共有___个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
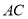 平分
平分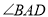 ,
, 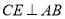 于
于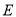 ,
, 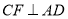 于
于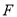 ,且
,且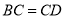 .
.(
 )求证:
)求证: 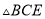 ≌
≌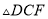 .
.(
 )若
)若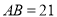 ,
, 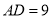 ,
, 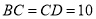 ,求
,求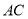 的长.
的长.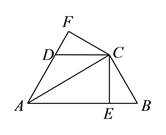
-
科目: 来源: 题型:
查看答案和解析>>【题目】两学生利用温差测某座山峰的高度,在山顶测得温度是2℃,在山脚测得温度是4℃,已知山峰高度每增加100米,气温大约下降0.6℃,这座山峰的高度大约是______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P(x,y),若点Q的坐标为(x+ay,ax+y)(其中a为常数,且a≠0),则称Q是点P的“a系联动点”.例如:点P(1,2)的“3系联动点”Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“
 系联动点”的坐标是(
系联动点”的坐标是( ,0),则点P的坐标为 ;
,0),则点P的坐标为 ;(2)若点P(x,y)的“a系联动点”与“
 系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;(3)在(2)的条件下,点P不与原点重合,点P的“a系联动点”为点Q,且PQ的长度为OP长度的3倍,求a的值.
相关试题

