【题目】阅读以下材料,并按要求完成相应的任务.
课题学习:如何解一元二次不等式?
例题:解一元二次不等式![]() .
.
解:![]()
![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
![]() 的解集为
的解集为![]() 或
或![]() .
.
即:一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
任务:(1)上面解一元二次不等式的过程中体现出了数学的一些基本思想方法,请在下列选项中选出你认为正确的一项:_____ ;(填选项即可)
A.分类讨论思想;B.数形结合思想;C.公理化思想;D.函数思想
(2)求一元二次不等式![]() 的解集为:_____ ;(直接填写结果,不写解答过程)
的解集为:_____ ;(直接填写结果,不写解答过程)
(3)仿照例题中的数学思想方法,求分式不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3) ![]() ;
;
【解析】
(1)根据解题过程可得分为同正、同负两类进行讨论,问题得解;
(2)类比例题解题过程,根据有理数的乘法法则“两数相乘,同号得正”分类讨论,求出不等式组的解集即可;
(3)类比例题,根据有理数的除法法则“两数相除,异号得负”分类讨论,求出不等式组的解集即可.
解:(1)上面解题过程中根据有理数的乘法法则“两数相乘,同号得正”,分为同正和同负两种情况进行,故选![]() ;
;
(2)由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
∴![]() 的解集为
的解集为![]() 或
或![]() ;
;
(3)由有理数的除法法则“两数相除,异号得负”,有
![]() ,
,![]() ,
,
解不等式组![]() 得:无解,
得:无解,
解不等式组![]() 得:
得:![]()
![]() 分式不等式
分式不等式![]() 的解集为:
的解集为:![]() .
.
-
科目: 来源: 题型:
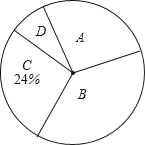
查看答案和解析>>【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节省空间,家里的饭碗一般是竖直摆放的,如果
 只饭碗(形状、大小相同)竖直摆放的高度为
只饭碗(形状、大小相同)竖直摆放的高度为 只饭碗竖直摆放的高度为
只饭碗竖直摆放的高度为 .如图所示,小颖家的碗橱每格的高度为
.如图所示,小颖家的碗橱每格的高度为 则一摞碗竖直放人橱柜时,每格最多能放________________________.
则一摞碗竖直放人橱柜时,每格最多能放________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图与图形变换
(尺规作图)(不写作法,保留作图痕迹)
如图,一辆汽车在直线形的公路上由点A向点B行驶,M,N 是分别位于公路两侧的村庄.
(1)在图1中求作一点P,使汽车行驶到此位置时,与村庄M,N的距离之和最小;

(2)在图2中求作一点Q,使汽车行驶到此位置时,与村庄 M,N 的距离相等.

(图形变换)
如图3所示,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(3)把△ABC 沿 BA 方向平移后,点 A 移到点
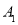 ,请你在网格中画出平移后得到的
,请你在网格中画出平移后得到的 ;
;(4)把
 绕点
绕点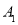 按逆时针方向旋转 90°,请你在网格中画出旋转后的
按逆时针方向旋转 90°,请你在网格中画出旋转后的 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西民间的雕刻艺术源远流长,主要以古代传统吉祥纹样为素材,以石雕、木雕砖雕等形式,来体现主人的高尚情操和文化修养以及人们的美好愿望.某木雕经销商购进“木象”和“木马”两种雕刻艺术品,购“木象”艺术品共用了
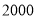 元,“木马”艺术品共用了
元,“木马”艺术品共用了 元已知“木马”每件的进价比“木象”每件的进价贵
元已知“木马”每件的进价比“木象”每件的进价贵 元,且购进“木象”“木马”的数量相同.
元,且购进“木象”“木马”的数量相同.
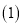 求每件“木象”、“木马”艺术品的进价;
求每件“木象”、“木马”艺术品的进价;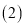 该经销商将购进的两种艺术品进行销售,“木象”的销售单价为
该经销商将购进的两种艺术品进行销售,“木象”的销售单价为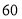 元,“木马”的销售单价为
元,“木马”的销售单价为 元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于
元,销售过程中发现“木象”的销量不好,经销商决定:“木象”销售一定数量后,将剩余的“木象”按原销售单价的七折销售;“木马”的销售单价保持不变要使两种艺术品全部售完后共获利不少于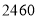 元,问“木象”按原销售单价应至少销售多少件?
元,问“木象”按原销售单价应至少销售多少件? -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
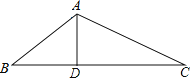
A. 20°B. 30°C. 45°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
相关试题

