【题目】![]() 问题发现
问题发现
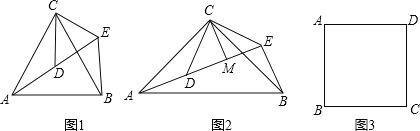
如图![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接BE.
在同一直线上,连接BE.
填空:
![]() 的度数为______;
的度数为______;
![]() 线段
线段![]() 之间的数量关系为______.
之间的数量关系为______.
![]() 拓展探究
拓展探究
如图![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上,CM为
在同一直线上,CM为![]() 中DE边上的高,连接BE,请判断
中DE边上的高,连接BE,请判断![]() 的度数及线段
的度数及线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
![]() 解决问题
解决问题
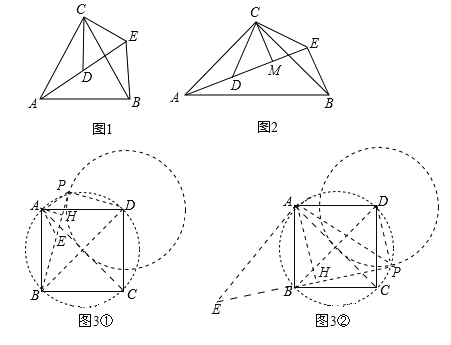
如图3,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.
参考答案:
【答案】![]() ;
;![]() ;
;![]() ,理由见解析;
,理由见解析; ![]() 点A到BP的距离为
点A到BP的距离为![]() 或
或![]() .
.
【解析】分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由PD=1可得:点P在以点D为圆心,1为半径的圆上;由∠BPD=90°可得:点P在以BD为直径的圆上.显然,点P是这两个圆的交点,由于两圆有两个交点,接下来需对两个位置分别进行讨论.然后,添加适当的辅助线,借助于(2)中的结论即可解决问题.
详解:(1)①如图1.∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵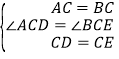 ,
,
∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC.
∵△DCE为等边三角形,∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC﹣∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,∴AD=BE.
故答案为:AD=BE.
(2)∠AEB=90°,AE=BE+2CM.
理由:如图2.∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵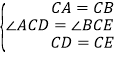 ,
,
∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,∴∠ADC=135°,∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.
(3)点A到BP的距离为![]() 或
或![]() .
.
理由如下:
∵PD=1,∴点P在以点D为圆心,1为半径的圆上.
∵∠BPD=90°,∴点P在以BD为直径的圆上,∴点P是这两圆的交点.
①当点P在如图3①所示位置时,连接PD、PB、PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交BP于点E,如图3①.
∵四边形ABCD是正方形,∴∠ADB=45°.AB=AD=DC=BC=![]() ,∠BAD=90°,∴BD=2.
,∠BAD=90°,∴BD=2.
∵DP=1,∴BP=![]() .
.
∵∠BPD=∠BAD=90°,∴A、P、D、B在以BD为直径的圆上,∴∠APB=∠ADB=45°,∴△PAE是等腰直角三角形.
又∵△BAD是等腰直角三角形,点B、E、P共线,AH⊥BP,∴由(2)中的结论可得:BP=2AH+PD,∴![]() =2AH+1,∴AH=
=2AH+1,∴AH=![]() .
.
②当点P在如图3②所示位置时,连接PD、PB、PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交PB的延长线于点E,如图3②.
同理可得:BP=2AH﹣PD,∴![]() =2AH﹣1,∴AH=
=2AH﹣1,∴AH=![]() .
.
综上所述:点A到BP的距离为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆普通票价20元
 张,暑假为了促销,新推出两种优惠卡:
张,暑假为了促销,新推出两种优惠卡: 金卡售价600元
金卡售价600元 张,每次凭卡不再收费.
张,每次凭卡不再收费. 银卡售价150元
银卡售价150元 张,每次凭卡另收10元.
张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数
 设游泳x次时,所需总费用为y元
设游泳x次时,所需总费用为y元 分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
分别写出选择银卡、普通票消费时,y与x之间的函数关系式; 在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;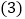 请根据函数图象,直接写出选择哪种消费方式更合算.
请根据函数图象,直接写出选择哪种消费方式更合算.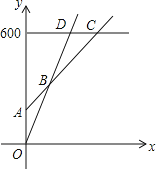
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=25°,求∠ACB的度数.
(2)若∠ACB=140°,求∠DCE的度数.
(3)猜想∠ACB与∠DCE的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点
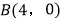 、
、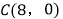 、
、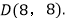 抛物线
抛物线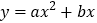 过A、C两点.
过A、C两点.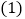 直接写出点A的坐标,并求出抛物线的解析式;
直接写出点A的坐标,并求出抛物线的解析式;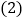 动点P从点A出发
动点P从点A出发 沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动
沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动 速度均为每秒1个单位长度,运动时间为t秒
速度均为每秒1个单位长度,运动时间为t秒 过点P作
过点P作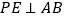 交AC于点E.
交AC于点E. 过点E作
过点E作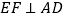 于点F,交抛物线于点
于点F,交抛物线于点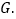 当t为何值时,线段EG最长?
当t为何值时,线段EG最长? 连接
连接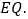 在点P、Q运动的过程中,判断有几个时刻使得
在点P、Q运动的过程中,判断有几个时刻使得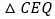 是等腰三角形?请直接写出相应的t值.
是等腰三角形?请直接写出相应的t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常繁琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100 ①
则S=100+99+98+…+1 ②
①+②,得(即左右两边分别相加):
2S=(1+100)+(2+99)+(3+98)+…+(100+1),
=
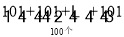 ,
,=100×101,
所以,S=
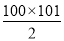 ③,
③,所以,1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.请你利用“倒序相加法”解答下面的问题.
(1)计算:1+2+3+…+101;
(2)请你观察上面解答过程中的③式及你运算过程中出现的类似③式,猜想:1+2+3+…+n= ;
(3)至少用两种方法计算:1001+1002+…+2000.
方法1:
方法2:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
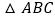 中,
中,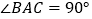 ,
,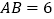 ,
, ,点D是BC的中点,将
,点D是BC的中点,将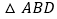 沿AD翻折得到
沿AD翻折得到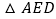 ,联结CE,那么线段CE的长等于_______.
,联结CE,那么线段CE的长等于_______.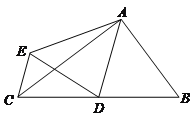
相关试题

