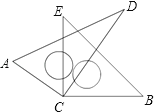
【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=25°,求∠ACB的度数.
(2)若∠ACB=140°,求∠DCE的度数.
(3)猜想∠ACB与∠DCE的关系,并说明理由.
参考答案:
【答案】(1)155°;(2)40°;(3)∠ACB与∠DCE互补.理由见解析.
【解析】
(1)由于是两直角三角形板重叠,重叠的部分就比90°+90°减少的部分,所以若∠DCE=25°,则∠ACB的度数为180°-25°=155°;
(2)与(1)同理,由∠ACB=140°,则∠DCE的度数为180°-∠ACB=40°;
(3)由于∠ACD=∠ECB=90°,重叠的度数就是∠ECD的度数,所以∠ACB+∠DCE=180°.
(1)∵∠ACD=∠ECB=90°,∠DCE=25°,
∴∠ACB=∠ACD+∠DCB
=∠ACD+∠ECB﹣∠DCE
=180°﹣25°
=155°;
(2)由(1)知∠ACB=180°﹣∠ECD,
∴∠ECD=180°﹣∠ACB=40°;
(3)∠ACB+∠DCE=180°,
理由:∵∠ACB=∠ACD+∠DCB=90°+90°﹣∠DCE.
∴∠ACB+∠DCE=180°,即∠ACB与∠DCE互补.
-
科目: 来源: 题型:
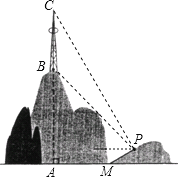
查看答案和解析>>【题目】如图,山顶建有一座铁塔,塔高
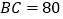 米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为
米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为 ,塔顶C点的仰角为
,塔顶C点的仰角为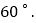 已测得小山坡的坡角为
已测得小山坡的坡角为 ,坡长
,坡长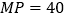 米
米 求山的高度
求山的高度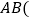 精确到1米
精确到1米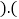 参考数据:
参考数据: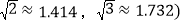
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆普通票价20元
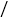 张,暑假为了促销,新推出两种优惠卡:
张,暑假为了促销,新推出两种优惠卡: 金卡售价600元
金卡售价600元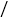 张,每次凭卡不再收费.
张,每次凭卡不再收费. 银卡售价150元
银卡售价150元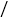 张,每次凭卡另收10元.
张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数
 设游泳x次时,所需总费用为y元
设游泳x次时,所需总费用为y元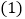 分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
分别写出选择银卡、普通票消费时,y与x之间的函数关系式; 在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标; 请根据函数图象,直接写出选择哪种消费方式更合算.
请根据函数图象,直接写出选择哪种消费方式更合算.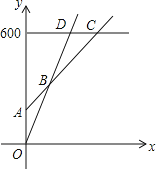
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 问题发现
问题发现如图
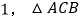 和
和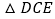 均为等边三角形,点
均为等边三角形,点 在同一直线上,连接BE.
在同一直线上,连接BE.填空:
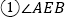 的度数为______;
的度数为______; 线段
线段 之间的数量关系为______.
之间的数量关系为______. 拓展探究
拓展探究如图
 和
和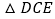 均为等腰直角三角形,
均为等腰直角三角形,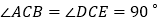 ,点
,点 在同一直线上,CM为
在同一直线上,CM为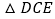 中DE边上的高,连接BE,请判断
中DE边上的高,连接BE,请判断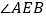 的度数及线段
的度数及线段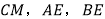 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. 解决问题
解决问题如图3,在正方形ABCD中,
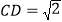 ,若点P满足
,若点P满足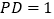 ,且
,且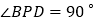 ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.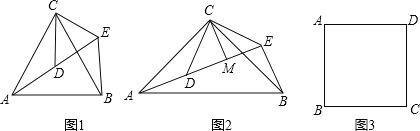
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点
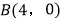 、
、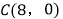 、
、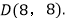 抛物线
抛物线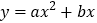 过A、C两点.
过A、C两点.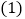 直接写出点A的坐标,并求出抛物线的解析式;
直接写出点A的坐标,并求出抛物线的解析式;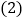 动点P从点A出发
动点P从点A出发 沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动
沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动 速度均为每秒1个单位长度,运动时间为t秒
速度均为每秒1个单位长度,运动时间为t秒 过点P作
过点P作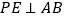 交AC于点E.
交AC于点E. 过点E作
过点E作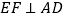 于点F,交抛物线于点
于点F,交抛物线于点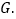 当t为何值时,线段EG最长?
当t为何值时,线段EG最长? 连接
连接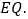 在点P、Q运动的过程中,判断有几个时刻使得
在点P、Q运动的过程中,判断有几个时刻使得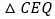 是等腰三角形?请直接写出相应的t值.
是等腰三角形?请直接写出相应的t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常繁琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100 ①
则S=100+99+98+…+1 ②
①+②,得(即左右两边分别相加):
2S=(1+100)+(2+99)+(3+98)+…+(100+1),
=
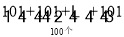 ,
,=100×101,
所以,S=
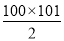 ③,
③,所以,1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.请你利用“倒序相加法”解答下面的问题.
(1)计算:1+2+3+…+101;
(2)请你观察上面解答过程中的③式及你运算过程中出现的类似③式,猜想:1+2+3+…+n= ;
(3)至少用两种方法计算:1001+1002+…+2000.
方法1:
方法2:
相关试题

