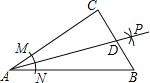
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以一个定长为半径画弧,两弧交于点P,作射线AP交BC于点D.若AC=8,BC=6,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
过点D作DE⊥AB于点E,由作图方法可知AP是∠BAC的平分线;由角平分线的性质定理可得CD=DE;由勾股定理求得AB的长;判定Rt△ADC≌Rt△ADE(HL);设CD=DE=x,在Rt△DEB中,由勾股定理求得x的值即可.
解:过点D作DE⊥AB于点E,如图所示:

∵∠C=90°,由作图方法可知AP是∠BAC的平分线,
∴CD=DE,设CD=DE=x,
在Rt△ABC中,
∵AC=8,BC=6,
∴AB=10.
∵∠C=∠AED=90°,AD=AD,DC=DE,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE=8,
∴EB=2,
在Rt△DEB中,
∵BD2=DE2+BE2,
∴(6﹣x)2=x2+22,
解得:x=![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AC,BD相交于O,则图中能够全等的三角形共有( )对.

A.4B.3C.2D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校的选修课教学,校教务处在七、八年级所有班级中,每班随机抽取了6名学生,并对他们的选修课喜欢程度情况进行了问卷调查,喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项.现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)若接核七、八年级共有700名学生,请你估境该年级学生中对远修课“不太喜欢”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:小刚根据学习函数的经验,对函数y=﹣2|x|+5的图象和性质进行了探究.下面是小刚的探究过程,请你解决相关问题:
(Ⅰ)在函数y=﹣2|x|+5中,自变量x可以是任意实数;
(Ⅱ)如表y与x的几组对应值:
X
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣3
﹣1
1
3
5
3
1
﹣1
﹣3
…
(Ⅲ)如图,在平面直角坐标系中,描出以表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
(1)若A(m,﹣11),B(8,﹣11)为该函数图象上不同的两点,则m= ;
(2)观察函数y=﹣2|x|+5的图象,写出该图象的一条性质 .
(3)直线y=kx+b(k≠0)经过点(﹣1,3)及点(4,﹣3),则当kx+b<﹣2|x|+5时,自变量x的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.方程x2-4x+2=0无实数根;
B.两条对角线互相垂直且相等的四边形是正方形
C.甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是
D.若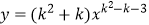 是反比例函数,则k的值为2或-1。
是反比例函数,则k的值为2或-1。
相关试题

