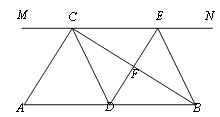
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
参考答案:
【答案】(1)证明见解析;(2)四边形BECD是菱形,理由见解析;(3)当∠A=45°时,四边形BECD是正方形,理由见解析.
【解析】试题分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)求出∠CDB=90°,再根据正方形的判定推出即可.
试题解析:(1)∵DE⊥BC, ∴∠DFB=90°, ∵∠ACB=90°, ∴∠ACB=∠DFB,
∴AC∥DE, ∵MN∥AB,即CE∥AD, ∴四边形ADEC是平行四边形, ∴CE=AD;
(2)四边形BECD是菱形, 理由是:∵D为AB中点, ∴AD=BD, ∵CE=AD,
∴BD=CE, ∵BD∥CE, ∴四边形BECD是平行四边形, ∵∠ACB=90°,D为AB中点,
∴CD=BD, ∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是: 解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°, ∴AC=BC, ∵D为BA中点, ∴CD⊥AB, ∴∠CDB=90°,
∵四边形BECD是菱形, ∴菱形BECD是正方形, 即当∠A=45°时,四边形BECD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘积等于m2-n2的式子是( )
A.(m-n)2
B.(m-n)(-m-n)
C.(n -m)(-m-n)
D.(m+n)(-m+n) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中不能用平方差公式计算的是( )
A.(x-2y)(2y+x)
B.(x-2y)(-2y+x)
C.(x+y)(y-x)
D.(2x-3y)(3y+2x) -
科目: 来源: 题型:
查看答案和解析>>【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.
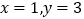 B.
B. 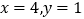 C.
C. 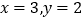 D.
D. 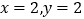
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是_______________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+b与反比例函数y=
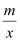 (x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴,y轴分别交干C,D两点.
(1)m= ,n= ;若M(xl,y1),N(x2,y2)是反比例函数图象上两点,且0<xl<x2,则yl y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,–3),则直线的函数表达式是__________.
相关试题

