【题目】为响应我市“中国梦”“宜宾梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
等级 | 频数 | 频率 |
一等奖 | a | 0.1 |
二等奖 | 10 | 0.2 |
三等奖 | b | 0.4 |
优秀奖 | 15 | 0.3 |
请你根据以上图表提供的信息,解答下列问题:
(1)a= , b= , n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
参考答案:
【答案】
(1)5;20;144
(2)解:列表得:
A | B | C | 王 | 李 | |
A | ﹣ | AB | AC | A王 | A李 |
B | BA | ﹣ | BC | B王 | B李 |
C | CA | CB | ﹣ | C王 | C李 |
王 | 王A | 王B | 王C | ﹣ | 王李 |
李 | 李A | 李B | 李C | 李王 | ﹣ |
∵共有20种等可能的情况,恰好是王梦、李刚的有2种情况,
∴恰好选中王梦和李刚两位同学的概率P= ![]() =
= ![]()
【解析】解:(1)观察统计表知,二等奖的有10人,频率为0.2, 故参赛的总人数为10÷0.2=50人,
a=50×0.1=5人,b=50×0.4=20.
n=0.4×360°=144°,
故答案为:5,20,144;
(1)首先利用频数、频率之间的关系求得参赛人数,然后乘以一等奖的频率即可求得a值,乘以三等奖的频率即可求得b值,用三等奖的频率乘以360°即可求得n值;(2)列表后即可将所有情况全部列举出来,从而求得恰好抽中者两人的概率;
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣2|+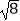 ﹣4sin45°﹣1﹣2
﹣4sin45°﹣1﹣2
(2)化简: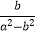
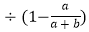 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.

(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取到最大值,则最大值为 ;(用含a、b的式子表示)。
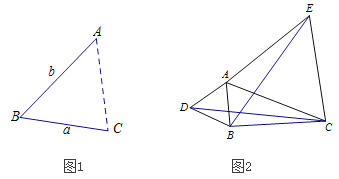
(2)如图2,若点A为线段BC外一动点,且BC=4,AB=2,分别以AB,AC为边,作等边
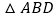 和等边
和等边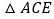 ,连接CD,BE.
,连接CD,BE. ①图中与线段BE相等的线段是线段 ,并说明理由;
②直接写出线段BE长的最大值为 。
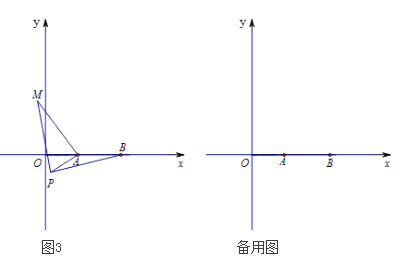
(3)如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值为 ,及此时点P的坐标为 。(提示:等腰直角三角形的三边长a、b、c满足a:b:c=1:1:
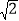 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年4月20日,我省芦山县发生7.0级强烈地震,造成大量的房屋损毁,急需大量帐篷.某企业接到任务,须在规定时间内生产一批帐篷.如果按原来的生产速度,每天生产120顶帐篷,那么在规定时间内只能完成任务的90%.为按时完成任务,该企业所有人员都支援到生产第一线,这样,每天能生产160顶帐篷,刚好提前一天完成任务.问规定时间是多少天?生产任务是多少顶帐篷?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=
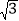 ,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
A. 2
B.

C.
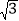
D.

相关试题

