【题目】如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD= . 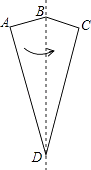
参考答案:
【答案】2+ ![]() 或4+2
或4+2 ![]()
【解析】解:如图1所示: 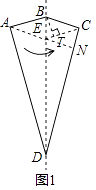
作AE∥BC,延长AE交CD于点N,过点B作BT⊥EC于点T,
当四边形ABCE为平行四边形,
∵AB=BC,
∴四边形ABCE是菱形,
∵∠A=∠C=90°,∠B=150°,BC∥AN,
∴∠ADC=30°,∠BAN=∠BCE=30°,
则∠NAD=60°,
∴∠AND=90°,
∵四边形ABCE面积为2,
∴设BT=x,则BC=EC=2x,
故2x×x=2,
解得:x=1(负数舍去),
则AE=EC=2,EN= ![]() =
= ![]() ,
,
故AN=2+ ![]() ,
,
则AD=DC=4+2 ![]() ;
;
如图2,当四边形BEDF是平行四边形,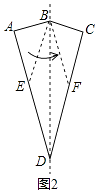
∵BE=BF,
∴平行四边形BEDF是菱形,
∵∠A=∠C=90°,∠B=150°,
∴∠ADB=∠BDC=15°,
∵BE=DE,
∴∠AEB=30°,
∴设AB=y,则BE=2y,AE= ![]() y,
y,
∵四边形BEDF面积为2,
∴AB×DE=2y2=2,
解得:y=1,故AE= ![]() ,DE=2,
,DE=2,
则AD=2+ ![]() ,
,
综上所述:CD的值为:2+ ![]() 或4+2
或4+2 ![]() .
.
故答案为:2+ ![]() 或4+2
或4+2 ![]() .
.
根据题意结合裁剪的方法得出符合题意的图形有两个,分别利用菱形的判定与性质以及勾股定理得出CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
 的线段的概率为( )
的线段的概率为( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1 , 0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
A.a(x1﹣x2)=d
B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d
D.a(x1+x2)2=d -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y=
 的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=
的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=  的图象经过点Q,则k= .
的图象经过点Q,则k= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2 , 则称点P′是点P关于⊙O的“反演点”. 如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数).

(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
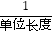
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
相关试题

