【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .
.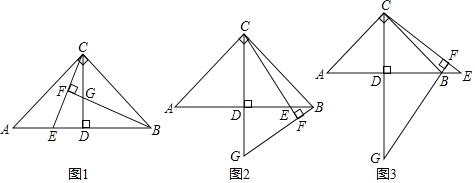
(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
(2)如图2,当点![]() 在线段
在线段![]() 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
参考答案:
【答案】(1)见解析;(2)AE=CG,理由见解析;(3)CG=AE
【解析】
(1)根据等腰直角三角形的性质得到∠A=∠ABC,根据同角的余角相等得到∠CBG=∠ACE,根据ASA证明△ACE≌△CBG,即可得出结论;
(2)同理即可证明△ACE≌△CBG,即可得出结论;
(3)同(2)可得∠A=∠GCB=45°,证得∠CGB=∠AEC,可证明△ACE≌△CBG,即可得出结论.
(1)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,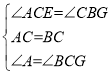 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(2)AE=CG;理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,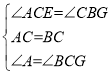 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(3)CG=AE.
证明:同(1)(2)可得∠A=∠GCB=45°,
∵BF⊥CE,
∴∠GDB=∠BFE=90°,
∵∠DBG=∠FBE,
∴∠CGB=∠AEC,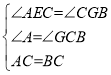 ,
,
∴△ACE≌△CBG(AAS),
∴CG=AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (
 a +b)(b -
a +b)(b - a)
a)C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小芳和小亮去商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元.
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任拿出200元学校奖励基金交给小芳,再次购买上述价格的钢笔和笔记本共48件作为奖品,奖励给校运动会中表现突出的同学,经双方协商,商店给出优惠是购买商品的总金额超出50的部分给打九折,请问小芳至少要买多少支钢笔? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
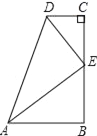
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
 为坐标原点,点
为坐标原点,点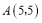 为第一象限内一点,点
为第一象限内一点,点 在
在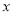 轴正半轴上,且
轴正半轴上,且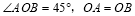 .
.
(1)求点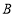 的坐标;
的坐标;
(2)动点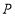 以每秒2个单位长度的速度,从点
以每秒2个单位长度的速度,从点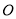 出发,沿
出发,沿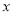 轴正半轴匀速运动,设点
轴正半轴匀速运动,设点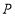 的运动时间为
的运动时间为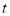 秒,
秒,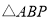 的面积为
的面积为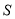 ,请用含有
,请用含有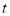 的式子表示
的式子表示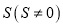 ,并直接写出
,并直接写出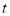 的取值范围;
的取值范围;
(3)如图2,在(2)的条件下,点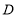 坐标为
坐标为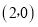 ,连接
,连接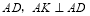 ,过点
,过点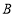 作
作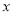 轴的垂线交
轴的垂线交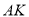 于点
于点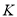 ,过点
,过点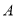 作
作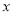 轴的平行线
轴的平行线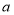 ,在点
,在点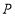 的运动过程中,直线
的运动过程中,直线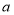 上是否存在一点
上是否存在一点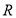 ,使
,使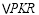 是以
是以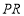 为腰的等腰直角三角形?若存在,求出点
为腰的等腰直角三角形?若存在,求出点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.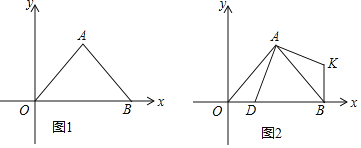
相关试题

