Question

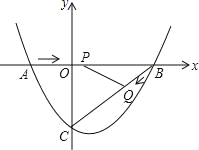
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx-3（a≠0）与x轴交于点A（-2，0）、B（4，0）两点，与y轴交于点C．

（1）求抛物线的解析式；

（2）点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？

（3）当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK：S△PBQ=5：2，求K点坐标．

Answer 1

【答案】(1) y=x2-x-3；(2) 运动1秒使△PBQ的面积最大，最大面积是；（3）K1（1，-），K2（3，-）．

【解析】

试题分析：（1）把点A、B的坐标分别代入抛物线解析式，列出关于系数a、b的解析式，通过解方程组求得它们的值；

（2）设运动时间为t秒．利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=-（t-1）2+．利用二次函数的图象性质进行解答；

（3）利用待定系数法求得直线BC的解析式为y=x-3．由二次函数图象上点的坐标特征可设点K的坐标为（m，m2-m-3）．

如图2，过点K作KE∥y轴，交BC于点E．结合已知条件和（2）中的结果求得S△CBK=．则根据图形得到：S△CBK=S△CEK+S△BEK=EKm+EK（4-m），把相关线段的长度代入推知：-m2+3m=．易求得K1（1，-），K2（3，-）．

试题解析：（1）把点A（-2，0）、B（4，0）分别代入y=ax2+bx-3（a≠0），得

，

解得，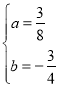

所以该抛物线的解析式为：y=x2-x-3；

（2）设运动时间为t秒，则AP=3t，BQ=t．

∴PB=6-3t．

由题意得，点C的坐标为（0，-3）．

在Rt△BOC中，BC==5．

如图1，过点Q作QH⊥AB于点H．

∴QH∥CO，

∴△BHQ∽△BOC，

∴，即，

∴HQ=t．

∴S△PBQ=PBHQ=（6-3t）t=-t2+t=-（t-1）2+．

当△PBQ存在时，0＜t＜2

∴当t=1时，

S△PBQ最大=．

答：运动1秒使△PBQ的面积最大，最大面积是；

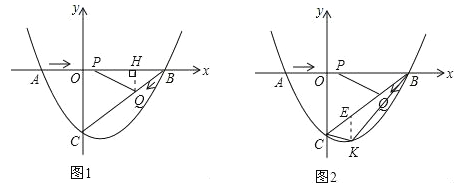
（3）设直线BC的解析式为y=kx+c（k≠0）．

把B（4，0），C（0，-3）代入，得

，

解得，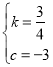

∴直线BC的解析式为y=x-3．

∵点K在抛物线上．

∴设点K的坐标为（m，m2-m-3）．

如图2，过点K作KE∥y轴，交BC于点E．则点E的坐标为（m，m-3）．

∴EK=m-3-（m2-m-3）=-m2+m．

当△PBQ的面积最大时，∵S△CBK：S△PBQ=5：2，S△PBQ=．

∴S△CBK=．

S△CBK=S△CEK+S△BEK=EKm+EK（4-m）

=×4EK

=2（-m2+m）

=-m2+3m．

即：-m2+3m=．

解得 m1=1，m2=3．

∴K1（1，-），K2（3，-）．