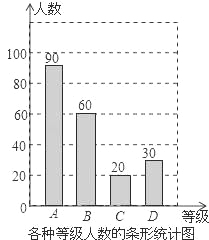
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
参考答案:
【答案】(1)30;(2)1000人;(3)![]() .
.
【解析】试题分析:(1)根据所有等级的百分比的和为1,则可计算出x=30,再利用A等级的人数除以它所占的百分比得到调查的总人数为200人,然后分别乘以30%和20%得到B等级和C等级人数,再将条形统计图补充完整;
(2)满足2≤t<4的人数就是B和C等级的人数,用2500乘以B、C两等级所占的百分比的和即可;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图展示所有20种等可能的结果数,其中选出的2人来自不同小组占12种,然后利用概率公式求解.
试题解析:(1)∵x%+15%+10%+45%=1,
∴x=30;
∵调查的总人数=90÷45%=200(人),
∴B等级人数=200×30%=60(人);C等级人数=200×10%=20(人),
如图:
(2)2500×(10%+30%)=1000(人),
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图为:
 ,
,
共有20种等可能的结果数,其中选出的2人来自不同小组占12种,
所以选出的2人来自不同小组的概率=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个既是轴对称图形又是中心对称图形的几何图形,这个图形可以是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若-xn+1与2x2n-1是同类项,则n=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:

(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?被调查的学生每人一周零花钱数额的中位数是多少元?
(3)为捐助贫困山区儿童学习,全校1000名学生每人自发地捐出一周的零花钱.请估算全校学生共捐款多少元?
-
科目: 来源: 题型:
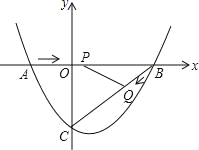
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①同位角相等; ②内错角相等 ; ③对顶角相等 ;④邻补角互补;⑤同旁内角互补
其中真命题的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

相关试题

