【题目】如图,抛物线y=ax2+bx过A(﹣4,0),B(﹣1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的函数表达式;
(2)写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于x轴的下方,当△ABP的面积为15时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时点N的坐标.
参考答案:
【答案】(1)y=﹣x2﹣4x;(2)3;(3)点P坐标为(﹣6,﹣12)或(1,﹣5);(4)N点坐标为(2,0)或(﹣4,0)或(﹣2,0)或(4,0).
【解析】分析:
(1)将点A、B的坐标代入y=ax2+bx中列出关于a、b的方程组,解方程组求得a、b的值即可得到抛物线的解析式y=﹣x2﹣4x;
(2)将(1)中抛物线的解析式化为“顶点式”得到抛物线的对称轴,结合点B的坐标即可求得点C的坐标,这样由A、B、C三点的坐标即可求得S△ABC的值;
(3)如下图1,过点P作PF垂直x轴,交直线AB于点F,先由A、B的坐标求得直线AB的解析式y=x+4,设点P的横坐标为m,则点P的坐标为(m,﹣m2﹣4m),点F的坐标为(m,m+4),由此可得PF= m2+5m+4,然后由S△PAB=S△PFB-S△PFA=15可得:![]() ×(m2+5m+4)×[(-1-m)-(-4-m)]=15,解此方程求得m的值即可得到点P的坐标;
×(m2+5m+4)×[(-1-m)-(-4-m)]=15,解此方程求得m的值即可得到点P的坐标;
(4)当以点C、M、N为顶点的三角形为等腰直角三角形时,分点C、M、N分别为直角顶点三类情况进行讨论:I、①M为直角顶点,且M在x轴上方;②M为直角顶点,且M在x轴的下方;II、①N为直角顶点,且N在y轴的右侧;②N为直角顶点,且N在y轴的左侧;III、C为直角顶点;根据上述情况画出对应的图形,再结合已知条件进行分析解答即可.
详解:
(1)把点A(﹣4,0),B(﹣1,3)代入抛物线y=ax2+bx中,
得![]() ,解得
,解得![]() ,
,
∴抛物线表达式为y=﹣x2﹣4x;
(2)∵y=﹣x2+4x=﹣(x+2)2+4,
∴抛物线对称轴为x=﹣2,
∵点C和点B关于对称轴对称,点B的坐标为(﹣1,3),
∴C(﹣3,3),
∴BC=2,
∴S△ABC=![]() ×2×3=3;
×2×3=3;
(3)如图1,过P点作PF垂直x轴,交直线AB于点F,
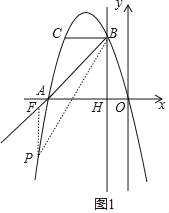
∵A(﹣4,0),B(﹣1,3),
设直线AB的解析式为y=kx+b,
则![]() ,解得
,解得![]() ,
,
即直线AB的解析式为y=x+4,
设点P(m,﹣m2﹣4m),则F(m,m+4),
∴PF=m+4+m2+4m=m2+5m+4.
∴S△PAB=![]() ×(m2+5m+4)×3=15,
×(m2+5m+4)×3=15,
m2+5m﹣6=0,
解得m1=﹣6,m2=1,
∴点P坐标为(﹣6,﹣12)或(1,﹣5);
(4)以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2,CM=MN,∠CMN=90°,
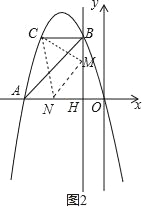
则△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴ON=OH+NH=2,
∴N(﹣2,0);
②以点M为直角顶点且M在x轴下方时,如图3,

作辅助线,构建如图所示的两直角三角形:Rt△NEM和Rt△MDC,
得Rt△NEM≌Rt△MDC,
∴EM=CD=5,
∵OH=1,
∴ON=NH﹣OH=5﹣1=4,
∴N(4,0);
③以点N为直角顶点且N在y轴右侧时,如图4,CN=MN,∠MNC=90°,作辅助线,
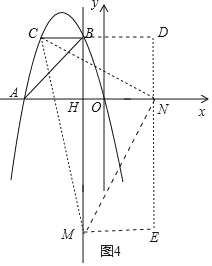
同理得Rt△NEM≌Rt△MDC,
∴ME=NH=DN=3,
∴ON=3﹣1=2,
∴N(2,0);
④以点N为直角顶点且N在y轴左侧时,作辅助线,如图5,
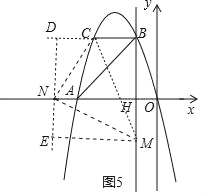
同理得ME=DN=NH=3,
∴ON=1+3=4,
∴N(﹣4,0);
⑤以C为直角顶点时,由于点C(-3,3)到x轴的距离和到抛物线对称轴x=-2的距离不相等,所以此时不能构成满足条件的等腰直角三角形;
综上可知当△CMN为等腰直角三角形时N点坐标为(2,0)或(﹣4,0)或(﹣2,0)或(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个三角形,分别连接这个三角形三边的中点得到图b;再分别连接图b中间小三角形的三边的中点,得到图c
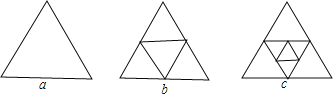
(1)图b有 个三角形,图c有 个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形(用n的代数式表示结论).
(3)当n=10时,第10个图形中有多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC中,AB=AC,点D是AC上一点。点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接CF
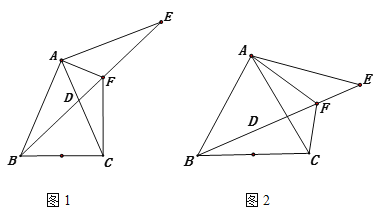
(1)如图1,找到与∠CFB相等的角,并证明
(2)如图2,如当∠ABC=60°,AF=m,EF=n时,求FB的长(用含m、n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RI△ABC中,∠C=90°,AC=BC=4cm,点P从点A出发沿线段AB以
 cm/s的速度向点B运动,设运动时间为ts.过点P作PD⊥AB,PD与△ABC的腰相交于点D.
cm/s的速度向点B运动,设运动时间为ts.过点P作PD⊥AB,PD与△ABC的腰相交于点D.(1)当t=(4-2
 )s时,求证:△BCD≌△BPD;
)s时,求证:△BCD≌△BPD;(2)当t为何值时,S△APD=3S△BPD,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.

(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为
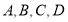 四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)求本次抽查的学生共有______人;
(2)将条形统计图和扇形统计图补充完整;
(3)扇形统计图中“
 ”所在扇形圆心角的度数为______;
”所在扇形圆心角的度数为______;(4)估计全校“
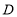 ”等级的学生有______人
”等级的学生有______人
相关试题

