【题目】已知关于![]() 的一元二次方程x2 +(2m+1)x+m2-4=0.
的一元二次方程x2 +(2m+1)x+m2-4=0.
(1)若此方程有两个不相等的实数根,求m的取值范围.
(2)若方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形,求这个四边形的周长.
参考答案:
【答案】(1)m>﹣![]() ;(2)15.
;(2)15.
【解析】【试题分析】(1)根据方程有两个不相等的实数根,则![]() ,即
,即![]() >0,得m>﹣
>0,得m>﹣![]() ;
;
(2)方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形,则这个方程有两个相等的实数根,即![]() ,即m=-
,即m=-![]() , 则方程x2 +(2m+1)x+m2-4=0为
, 则方程x2 +(2m+1)x+m2-4=0为![]() 根据韦达定理,得
根据韦达定理,得![]() ,∴x1=x2=
,∴x1=x2=![]() , 则菱形的周长是边长乘以4,得15.
, 则菱形的周长是边长乘以4,得15.
【试题解析】
(1) ,
,
当4m+17>0时,方程有两个不相等的实数根,
∴当m>﹣![]() 时,方程有两个不相等的实数根
时,方程有两个不相等的实数根
(2)∵方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形
∴方程有两个相等的实数根∴4m+17=0,得m=-![]() , 则方程x2 +(2m+1)x+m2-4=0为
, 则方程x2 +(2m+1)x+m2-4=0为![]() 根据韦达定理,得
根据韦达定理,得![]() ,∴x1=x2=
,∴x1=x2=![]() , ∴周长=15.
, ∴周长=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先阅读,再填空:
(x+5)(x+6)=x2+11x+30;
(x-5)(x-6)=x2-11x+30;
(x-5)(x+6)=x2+x-30;
(x+5)(x-6)=x2-x-30.
观察上面的算式,根据规律,直接写出下列各式的结果:
(a+90)(a-100)=____________; (y-80)(y-90)=____________.
(2)先阅读,再填空:
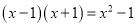 ;
;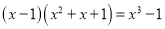 ;
;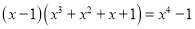 ;
;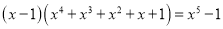 .
.观察上面各式:①由此归纳出一般性规律:
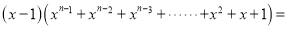 ________;
________;②根据①直接写出1+3+32+…+367+368的结果 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
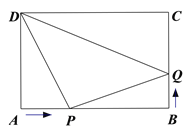
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
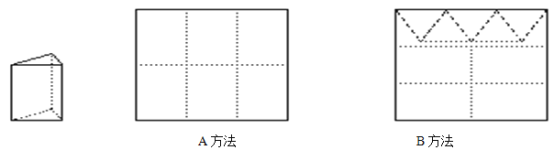
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

