【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.

参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的性质得出∠1=∠ABE,∠2=∠ADF。根据四边形内角和定理可得∠ABC+∠ADC=180°,即2(∠1+∠2)=180°,从而得出答案;(2)、根据三角形内角和定理可得∠DFC+∠2=90°,结合第一题的结论得出∠1=∠DFC,从而得出答案.
试题解析:(1)、∵BE,DF分别是∠ABC,∠ADC的平分线, ∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°, ∴∠ABC+∠ADC=180°, ∴2(∠1+∠2)=180°, ∴∠1+∠2=90°;
(2)、在△FCD中,∵∠C=90°, ∴∠DFC+∠2=90°, ∵∠1+∠2=90°,
∴∠1=∠DFC, ∴BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2
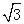 ,求阴影部分的面积.
,求阴影部分的面积.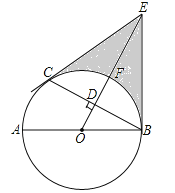
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先阅读,再填空:
(x+5)(x+6)=x2+11x+30;
(x-5)(x-6)=x2-11x+30;
(x-5)(x+6)=x2+x-30;
(x+5)(x-6)=x2-x-30.
观察上面的算式,根据规律,直接写出下列各式的结果:
(a+90)(a-100)=____________; (y-80)(y-90)=____________.
(2)先阅读,再填空:
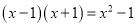 ;
;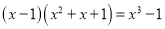 ;
;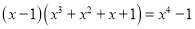 ;
;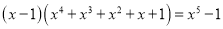 .
.观察上面各式:①由此归纳出一般性规律:
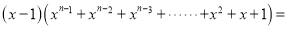 ________;
________;②根据①直接写出1+3+32+…+367+368的结果 ____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
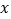 的一元二次方程x2 +(2m+1)x+m2-4=0.
的一元二次方程x2 +(2m+1)x+m2-4=0.(1)若此方程有两个不相等的实数根,求m的取值范围.
(2)若方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形,求这个四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
相关试题

