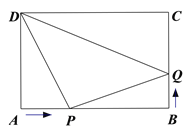
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
参考答案:
【答案】(1)3;(2)4.
【解析】【试题分析】(1)设t秒后点P、D的距离是点P、Q距离的2倍,即PD=2PQ
因为四边形ABCD是矩形,根据矩形的性质得,∠A=∠B=90°利用勾股定理得:PD2=AP2+AD2 ,PQ2=BP2+BQ2,由于PD2=4 PQ2,即82+(2t)2=4[(10-2t)2+t2],
解得:t1=3,t2=7(舍去),即t=3;
(2) 设x秒后△DPQ的面积是24cm2,根据矩形的面积等于三个直角三角形的面积加上24,即![]()
x1=x2=4,即4秒后,△DPQ的面积是24cm2.
【试题解析】
(1)设t秒后点P、D的距离是点P、Q距离的2倍,
∴PD=2PQ
∵四边形ABCD是矩形
∴∠A=∠B=90°
∴PD2=AP2+AD2 ,PQ2=BP2+BQ2
∵PD2=4 PQ2,∴82+(2t)2=4[(10-2t)2+t2],
解得:t1=3,t2=7;
∵t=7时10-2t<0,∴t=3
(2) 设x秒后△DPQ的面积是24cm2,
∴![]()
整理得x2-8x+16=0
解得x1=x2=4
即4秒后,△DPQ的面积是24cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
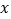 的一元二次方程x2 +(2m+1)x+m2-4=0.
的一元二次方程x2 +(2m+1)x+m2-4=0.(1)若此方程有两个不相等的实数根,求m的取值范围.
(2)若方程的两个根分别是平行四边形的一组邻边的长,该平行四边形为菱形,求这个四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
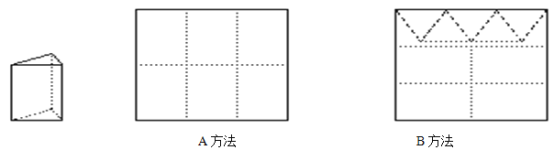
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线相交于P,∠A=m°,
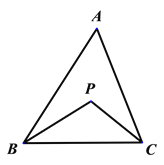
(1)若∠A=40°,求∠BPC的度数;
(2)设△ABC的外角∠CBD、∠BCE的平分线相交于Q, 且∠A=m°,求∠BQC的度数

(3)设△ABC的外角∠CBD、∠BCE的n等分线相交于R,且∠A=m°,∠CBR=
 ∠CBD,∠BCR=
∠CBD,∠BCR=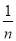 ∠BCE,求∠BRC的度数
∠BCE,求∠BRC的度数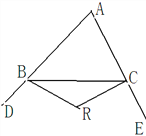
相关试题

