【题目】已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC对称,点E与点F关于BD对称,AC与BD相交于点G,则( ) 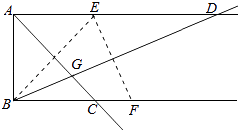
A.1+tan∠ADB= ![]()
B.2BC=5CF
C.∠AEB+22°=∠DEF
D.4cos∠AGB= ![]()
参考答案:
【答案】A
【解析】解:如图,连接CE,设EF与BD相交于点O, 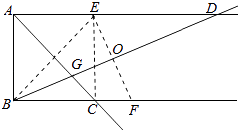
由轴对称性得,AB=AE,设为1,
则BE= ![]() =
= ![]() ,
,
∵点E与点F关于BD对称,
∴DE=BF=BE= ![]() ,
,
∴AD=1+ ![]() ,
,
∵AD∥BC,AB⊥AD,AB=AE,
∴四边形ABCE是正方形,
∴BC=AB=1,
1+tan∠ADB=1+ ![]() =1+
=1+ ![]() ﹣1=
﹣1= ![]() ,故A正确;
,故A正确;
CF=BF﹣BC= ![]() ﹣1,
﹣1,
∴2BC=2×1=2,
5CF=5( ![]() ﹣1),
﹣1),
∴2BC≠5CF,故B错误;
∠AEB+22°=45°+22°=67°,
∵BE=BF,∠EBF=∠AEB=45°,
∴∠BFE= ![]() =67.5°,
=67.5°,
∴∠DEF=∠BFE=67.5°,故C错误;
由勾股定理得,OE2=BE2﹣BO2=( ![]() )2﹣(
)2﹣( ![]() )2=
)2= ![]() ,
,
∴OE= ![]() ,
,
∵∠EBG+∠AGB=90°,
∠EBG+∠BEF=90°,
∴∠AGB=∠BEF,
又∵∠BEF=∠DEF
∴cos∠AGB= ![]() =
= ![]() =
= ![]() ,4cos∠AGB=2
,4cos∠AGB=2 ![]() ,故D错误.
,故D错误.
故选:A.
【考点精析】解答此题的关键在于理解轴对称的性质的相关知识,掌握关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2001年至2012年杭州市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图.由图得出如下四个结论:
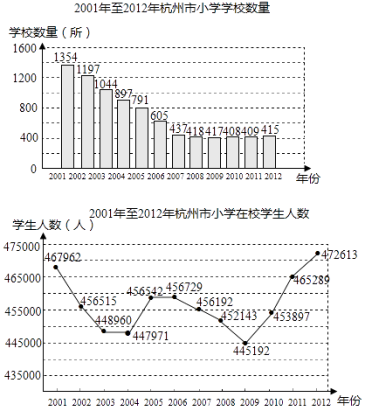
①学校数量2007年~2012年比2001~2006年更稳定;
②在校学生人数有两次连续下降,两次连续增长的变化过程;
③2009年的 大于1000;
大于1000;
④2009~2012年,相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中,正确的结论是( )
A.①②③④
B.①②③
C.①②
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)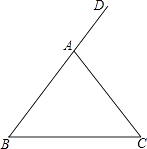
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明: 判断四边形AECF的形状并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75)
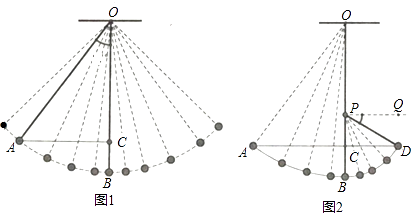
(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+5经过点B(3,9)和A(﹣6,m).
(1)求k,m的值;
(2)求△AOB的面积.

相关试题

