【题目】设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
参考答案:
【答案】y= ![]() x2﹣
x2﹣ ![]() x+2或y=﹣
x+2或y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
【解析】解:∵点C在直线x=2上,且到抛物线的对称轴的距离等于1, ∴抛物线的对称轴为直线x=1或x=3,
当对称轴为直线x=1时,设抛物线解析式为y=a(x﹣1)2+k,
将A(0,2),B(4,3)代入解析式,
则 ![]() ,
,
解得 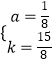 ,
,
所以,y= ![]() (x﹣1)2+
(x﹣1)2+ ![]() =
= ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
当对称轴为直线x=3时,设抛物线解析式为y=a(x﹣3)2+k,
将A(0,2),B(4,3)代入解析式,
则 ![]() ,
,
解得 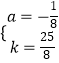 ,
,
所以,y=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
综上所述,抛物线的函数解析式为y= ![]() x2﹣
x2﹣ ![]() x+2或y=﹣
x+2或y=﹣ ![]() x2+
x2+ ![]() x+2.
x+2.
所以答案是:y= ![]() x2﹣
x2﹣ ![]() x+2或y=﹣
x+2或y=﹣ ![]() x2+
x2+ ![]() x+2.
x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC对称,点E与点F关于BD对称,AC与BD相交于点G,则( )
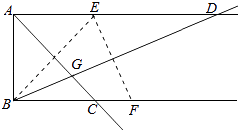
A.1+tan∠ADB=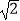
B.2BC=5CF
C.∠AEB+22°=∠DEF
D.4cos∠AGB=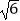
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75)
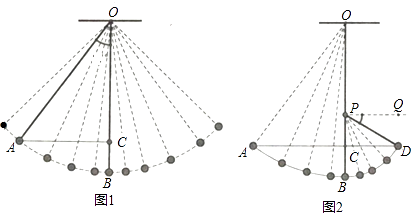
(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+5经过点B(3,9)和A(﹣6,m).
(1)求k,m的值;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B,C都在半径为r的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H.若BH=
 AC,则∠ABC所对的弧长等于(长度单位).
AC,则∠ABC所对的弧长等于(长度单位). -
科目: 来源: 题型:
查看答案和解析>>【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
36
52
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?
相关试题

