【题目】已知2001年至2012年杭州市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图.由图得出如下四个结论: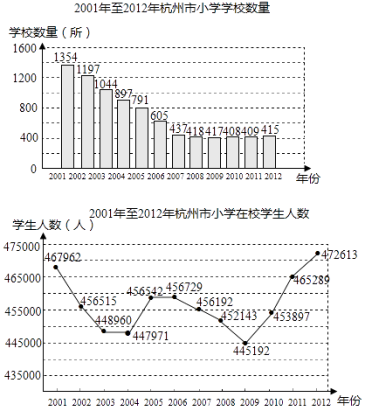
①学校数量2007年~2012年比2001~2006年更稳定;
②在校学生人数有两次连续下降,两次连续增长的变化过程;
③2009年的 ![]() 大于1000;
大于1000;
④2009~2012年,相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中,正确的结论是( )
A.①②③④
B.①②③
C.①②
D.③④
参考答案:
【答案】B
【解析】解:①根据条形统计图可知,学校数量2001~2006年下降幅度较大,最多1354所,最少605所,而2007年~2012年学校数量都是在400所以上,440所以下,故结论①正确;
②由折线统计图可知,在校学生人数有2001年~2003年、2006年~2009年两次连续下降,2004年~2006年、2009年~2012年两次连续增长的变化过程,故结论②正确;
③由统计图可知,2009年的在校学生445192人,学校数量417所,
所以2009年的 ![]() =
= ![]() =1067
=1067 ![]() >1000,故结论③正确;
>1000,故结论③正确;
④∵2009~2010年学校数量增长率为 ![]() ≈﹣2.16%,
≈﹣2.16%,
2010~2011年学校数量增长率为 ![]() ≈0.245%,
≈0.245%,
2011~2012年学校数量增长率为 ![]() ≈1.47%,
≈1.47%,
1.47%>0.245%>﹣2.16%,
∴2009~2012年,相邻两年的学校数量增长最快的是2011~2012年;
∵2009~2010年在校学生人数增长率为 ![]() ≈1.96%,
≈1.96%,
2010~2011年在校学生人数增长率为 ![]() ≈2.510%,
≈2.510%,
2011~2012年在校学生人数增长率为 ![]() ≈1.574%,
≈1.574%,
2.510%>1.96%>1.574%,
∴2009~2012年,相邻两年的在校学生人数增长最快的是2010~2011年,
故结论④错误.
综上所述,正确的结论是:①②③.
故选:B.
【考点精析】根据题目的已知条件,利用条形统计图和折线统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)计算:|﹣2|﹣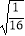 +(﹣2)﹣2﹣(
+(﹣2)﹣2﹣( 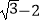 )0;
)0;
(2)解不等式组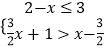 ,并求其最小整数解.
,并求其最小整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
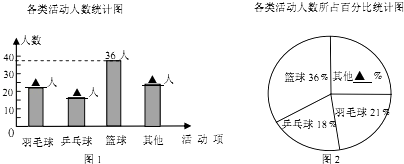
(1)学校采用的调查方式是;学校共选取了名学生;
(2)补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他%;
(3)该校共有1100名学生,请估计喜欢“篮球”的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数的自变量x满足
 ≤x≤2时,函数值y满足
≤x≤2时,函数值y满足  ≤y≤1,则这个函数可以是( )
≤y≤1,则这个函数可以是( )
A.y=
B.y=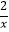
C.y=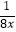
D.y=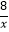
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)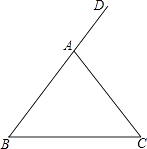
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明: 判断四边形AECF的形状并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC对称,点E与点F关于BD对称,AC与BD相交于点G,则( )
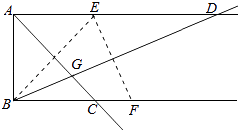
A.1+tan∠ADB=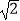
B.2BC=5CF
C.∠AEB+22°=∠DEF
D.4cos∠AGB=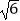
相关试题

