【题目】为解决中小学大班额问题,某县今年将改扩建部分中小学,根据预算,改扩建3所中学和2所小学共需资金6200万元,改扩建1所中学和3所小学共需资金4400万元
(1)改扩建1所中学和1所小学所需资金分别是多少万元?
(2)该县计划改扩建中小学共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过8400万元;地方财政投入资金不少于4000万元,其中地方财政投入到中小学的改扩建资金分别为每所500万元和300万元,请问共有哪几种改扩建方案?
参考答案:
【答案】(1)改扩建1所中学需要1400万元,改扩建1所小学需要1000万元;(2)共有2中改扩建方案,方案一:改扩建中学5所、小学5所;方案二:改扩建中学6所、小学4所.
【解析】
(1)设改扩建1所中学需要x万元,改扩建1所小学需要y万元,根据“改扩建3所中学和2所小学共需资金6200万元,改扩建1所中学和3所小学共需资金4400万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设改扩建m所中学,则改扩建(10-m)所小学,根据总价=单价×数量结合国家财政拨付资金不超过8400万元及地方财政投入资金不少于4000万元,即可得出关于m的一元一次不等式组,解之取其整数值即可得出各改扩建方案.
解:(1)设改扩建1所中学需要![]() 万元,改扩建1所小学需要
万元,改扩建1所小学需要![]() 万元,
万元,
依题意,得:![]() ,
,
解得:![]() .
.
答:改扩建1所中学需要1400万元,改扩建1所小学需要1000万元.
(2)设改扩建![]() 所中学,则改扩建
所中学,则改扩建![]() 所小学,
所小学,
依题意,得: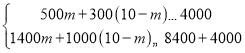 ,
,
解得:![]() .
.
![]() 为整数,
为整数,
![]() 或
或![]() ,
,
![]() 共有2中改扩建方案,方案一:改扩建中学5所、小学5所;方案二:改扩建中学6所、小学4所.
共有2中改扩建方案,方案一:改扩建中学5所、小学5所;方案二:改扩建中学6所、小学4所.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,点
中,点 是
是 的中点,延长
的中点,延长 ,
,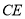 交于点
交于点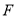 ,连结
,连结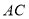 ,
,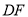 .
.(1)求证:四边形
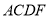 是平行四边形;
是平行四边形;(2)当
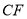 平分
平分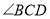 时,写出
时,写出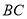 与
与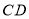 的数量关系,并说明理由.
的数量关系,并说明理由.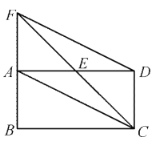
-
科目: 来源: 题型:
查看答案和解析>>【题目】信息化时代的到来,手机已经成为我们生活中不可缺少的一部分.为了解中学生在假期使用手机的情况(选项:
 .聊天;
.聊天; .游戏
.游戏 .学习;
.学习; .其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出).
.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出).
(1)这次被调查的学生有多少人?被调查的学生中,用手机学习的有多少人?
(2)将两个统计图补充完整;
(3)在扇形统计图中,请计算本项调查中用手机学习部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算用手机学习的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车销售公司4月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该汽车的进价为30万元,每多售出1辆,所有售出汽车的进价均降低0.1万元/辆,月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)若该公司当月售出5辆汽车,则每辆汽车的进价为 万元.
(2)若汽车的售价为31万/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数y=
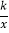 (k>1)和y=
(k>1)和y=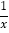 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=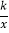 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=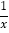 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=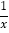 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y=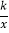 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式
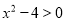 .
.解∵
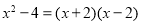 ,∴
,∴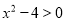 可化为
可化为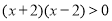 .
.由有理数的乘法法则:两数相乘,同号得正,得:①
 ②
②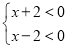
解不等式组①,得
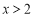 ,解不等式组②,得
,解不等式组②,得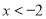
∴
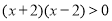 的解集为
的解集为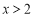 或
或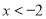 .
.即一元二次不等式
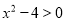 的解集为
的解集为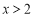 或
或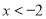 .
.(1)一元二次不等式
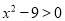 的解集为____________;
的解集为____________;(2)试解一元二次不等式
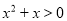 ;
;(3)试解不等式
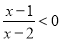 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)


结合统计图完成下列问题:
(1)扇形统计图中,表示12.5≤x<13部分的百分数是 ;
(2)请把频数分布直方图补充完整,这个样本数据的中位数落在第 组;
(3)哪一个图能更好地说明一半以上的汽车行驶的路程在13≤x<14之间?哪一个图能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车?
相关试题

