【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

参考答案:
【答案】(1)12米;(2)采用规格为1.00×1.00所需的费用较少
【解析】试题分析:(1)根据题意表示出长方形的长,进而利用长×宽=面积,求出即可;(2)分别计算出每一规格的地板砖所需的费用,然后比较即可.
试题解析:(1)设这地面矩形的长是xm,则依题意得: x(20﹣x)=96,
解得x1=12,x2=8(舍去),
答:这地面矩形的长是12米;
(2)规格为0.80×0.80所需的费用:96×(0.80×0.80)×55=8250(元).
规格为1.00×1.00所需的费用:96×(1.00×1.00)×80=7680(元).
因为8250<7680,
所以采用规格为1.00×1.00所需的费用较少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形、矩形、菱形、正方形共有的性质是( )
A. 对角线相等 B. 对角线互相平分
C. 对角线互相垂直 D. 对角形互相垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组在学习二次根式
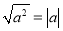 之后,研究了如下四个问题,其中不正确的是( )
之后,研究了如下四个问题,其中不正确的是( )A. 在a>1的条件下化简代数式
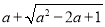 的结果为
的结果为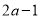
B. 当
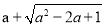 的值恒为定值时,字母a的取值范围是a≤1
的值恒为定值时,字母a的取值范围是a≤1C.
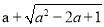 的值随a变化而变化, 当a取某个数值时,上述代数式的值可以为
的值随a变化而变化, 当a取某个数值时,上述代数式的值可以为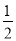
D. 若
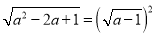 ,则字母a必须满足a≥1
,则字母a必须满足a≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0,如果AB=3,AO=2,那么AC的长等于______.
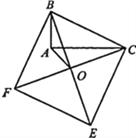
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3x2﹣75;
(2)x3y﹣4x2y2+4xy3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪种四边形的两条对角线互相垂直平分且相等( )
A. 矩形 B. 菱形 C. 平行四边形 D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知菱形ABCD的面积为15,顶点A在双曲线
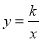 上,CD与y轴重合,且AB⊥x轴于B,AB=5.
上,CD与y轴重合,且AB⊥x轴于B,AB=5.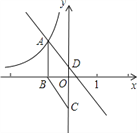
(1)求顶点A的坐标和k的值;
(2)求直线AD的解析式y1;
(3)在第二象限内,比较y与y1 的大小。
相关试题

