Question

【题目】如图，在直角坐标系中，已知菱形ABCD的面积为15，顶点A在双曲线上，CD与y轴重合，且AB⊥x轴于B，AB=5．

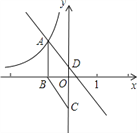
（1）求顶点A的坐标和k的值；

（2）求直线AD的解析式y1；

（3）在第二象限内，比较y与y1 的大小。

Answer 1

【答案】（1）顶点A的坐标为（－3，5），k的值为－15 ;（2）;

（3）当x<-3时，y<y1；当x=-3时，y=y1；当-3<x<0时，y>y1

【解析】（1）连接BD，作DE⊥AB，根据三角形的面积公式可得S菱形ABCD=2S△ABD，S△ABD=AB×ED，再由菱形ABCD的面积为15，AB=5，可求得DE的长，即可求得A点的坐标，从而求得k的值；
（2）设点D的坐标为（0，y），则可得AB=AD=5，根据勾股定理可列方程求得点D的坐标，设直线AD的解析式为y=k′x+b，根据待定系数法列方程组求解即可.
（1）连接BD，作DE⊥AB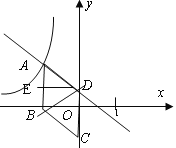

∴S菱形ABCD=2S△ABD，S△ABD=AB×ED，
∵菱形ABCD的面积为15，AB=5，
∴2××5×ED=15，解得DE=3，
∴点A的坐标为（-3，5）；
又∵点A在双曲线上，
∴，解得k=-15；
（2）设点D的坐标为（0，y）
∴AB=AD=5，
∴，解得y=9（舍去）或y=1，
∴点D的坐标为（0，1）．
设直线AD的解析式为y=k′x+b，
∵直线AD过A、D两点，
∴，解之得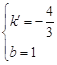
∴直线AD的解析式为.
（3）当x<-3时，y<y1；当x=-3时，y=y1；当--3<x<0时，y>y1 .

“点睛”待定系数法求函数关系式是函数问题中极为重要的方法，再中考中比较常见，一般难度不大，需熟练掌握.