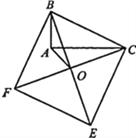
【题目】如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0,如果AB=3,AO=2,那么AC的长等于______.
参考答案:
【答案】2![]() +3.
+3.
【解析】在AC上截取CG=AB=3,连接OG,根据B、A、O、C四点共圆,推出∠ABO=∠ACO,证△BAO≌△CGO,推出OA=OG=2,∠AOB=∠COG,得出等腰直角三角形AOG,根据勾股定理求出AG,即可求出AC.
解:在AC上截取CG=AB=3,连接OG,
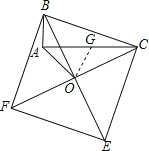
∵四边形BCEF是正方形,∠BAC=90°,
∴OB=OC,∠BAC=∠BOC=90°,
∴B、A、O、C四点共圆,
∴∠ABO=∠ACO,
在△BAO和△CGO中
BA=CG BA=CG,∠BAO=∠GCO,OB=OC,
∴△BAO≌△CGO(SAS),
∴OA=OG=2,∠AOB=∠COG,
∵∠BOC=∠COG+∠BOG=90°,
∴∠AOG=∠AOB+∠BOG=90°,
即△AOG是等腰直角三角形,
由勾股定理得:AG=![]() ,
,
即AC=2![]() +3.
+3.
故答案是:2![]() +3.
+3.
“点睛”本题主要考查对勾股定理,正方形的性质,直角三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能熟练地运用这些性质进行推理和计算是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(2m﹣6)x|m|﹣2=m2是关于x的一元一次方程,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形、矩形、菱形、正方形共有的性质是( )
A. 对角线相等 B. 对角线互相平分
C. 对角线互相垂直 D. 对角形互相垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组在学习二次根式
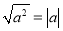 之后,研究了如下四个问题,其中不正确的是( )
之后,研究了如下四个问题,其中不正确的是( )A. 在a>1的条件下化简代数式
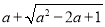 的结果为
的结果为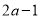
B. 当
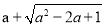 的值恒为定值时,字母a的取值范围是a≤1
的值恒为定值时,字母a的取值范围是a≤1C.
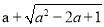 的值随a变化而变化, 当a取某个数值时,上述代数式的值可以为
的值随a变化而变化, 当a取某个数值时,上述代数式的值可以为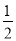
D. 若
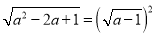 ,则字母a必须满足a≥1
,则字母a必须满足a≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3x2﹣75;
(2)x3y﹣4x2y2+4xy3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪种四边形的两条对角线互相垂直平分且相等( )
A. 矩形 B. 菱形 C. 平行四边形 D. 正方形
相关试题

