搜索
【题目】如图所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．
参考答案：
【答案】36．
【解析】
试题分析：如图所示，连接AC，可得△ABC与△DAC均为直角三角形，进而可求解四边形的面积．
试题解析：连接AC，
因为AB=4，BC=3，CD=13，DA=12，∠B=90°，
所以AC2=AB2-+BC2 ，
=42+32，
=16+9，
=25，
所以AC=5，
又因CD2-DA2，
=132-122，
=169-144，
=25，
=AC2，
所以△DAC为直角三角形，
因此S四边形ABCD的面积=S△ABC+S△DAC，
=
AB×BC+AD×AC，
=×4×3+×12×5，
=6+30，
=36．
答：四边形ABCD的面积等于36．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”．将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f（a）．例如：a=12，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为21+12=33，和与11的商为3311=3，所以f（12）=3．
根据以上定义，回答下列问题：
（1）填空：
①下列两位数：40，42，44中，“迥异数”为 ；
②计算：f（23）= ．
（2）如果一个“迥异数”b的十位数字是k，个位数字是2（k+1），且f（b）=11，请求出“迥异数”b．
（3）如果一个“迥异数”c，满足c5f（c）30，请直接写出满足条件的c的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，过对角线BD上点P作直线EF，GH分别平行于AB，BC，那么图中共有（ ）对面积相等平行四边形．
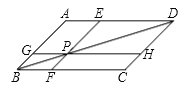
A. 1对B. 2对C. 3对D. 4对
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )
A.
B. 
C. 3 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF，连接AF，BF，DE，CE，分别交于H，G．求证：
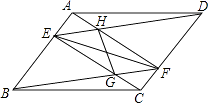
（1）EF与GH互相平分；
（2）在不添加任何辅助线和字母的条件下，请直接写出图中所有的全等的三角形． -
科目： 来源： 题型：
查看答案和解析>>【题目】六一前夕，某幼儿园园长到厂家选购A、B两种品牌的儿童服装，每套A品牌服装进价比B品牌服装每套进价多25元，用2000元购进A种服装数量是用750元购进B种服装数量的2倍．
（1）求A、B两种品牌服装每套进价分别为多少元？
（2）该服装A品牌每套售价为130元，B品牌每套售价为95元，服装店老板决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套，两种服装全部售出后，可使总的获利超过1200元，则最少购进A品牌的服装多少套？ -
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数)，随机对该年级50名学生进行了调查，根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值，如最左边第一组的次数x为：
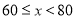，则以下说法正确的是( )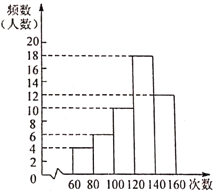
A. 跳绳次数最多的是160次
B. 大多数学生跳绳次数在140-160范围内
C. 跳绳次数不少于100次的占80%
D. 由样本可以估计全年级800人中跳绳次数在60-80次的大约有70人
相关试题
