【题目】如图,在ABCD中,过对角线BD上点P作直线EF,GH分别平行于AB,BC,那么图中共有( )对面积相等平行四边形.
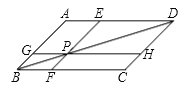
A. 1对B. 2对C. 3对D. 4对
参考答案:
【答案】C
【解析】
平行四边形的对角线将平行四边形分成两个面积相等的三角形.所以三角形ABD的面积等于三角形BCD的面积.三角形BFP的面积等于BGP的面积,三角形PED的面积等于三角形HPD的面积,从而可得到四边形PFCH的面积等于四边形AGPE的面积,同时加上一个公共的平行四边形,可以得出答案有三个.
∵ABCD为平行四边形,BD为对角线,∴△ABD的面积等于△BCD的面积,同理△BFP的面积等于△BGP的面积,△PED的面积等于△HPD的面积.
∵△BCD的面积减去△BFP的面积和PHD的面积等于平行四边形PFCH的面积,△ABD的面积减去△GBD和△EPD的面积等于平行四边形AGPE的面积,∴平行四边形PFCH的面积=平行四边形AGPE的面积,∴同时加上平行四边形PHDE和BFPG,可以得出平行四边形AGHD面积和平行四边形EFCD面积相等,平行四边形ABFE和平行四边形BCHG面积相等.
所以有3对面积相等的平行四边形.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
 的解是
的解是 ,
, ;
; 即
即 的解是
的解是 ;
; 的解是
的解是 ,
, ;
; 的解是
的解是 ,
, ;
;
 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21+12=33,和与11的商为3311=3,所以f(12)=3.
根据以上定义,回答下列问题:
(1)填空:
①下列两位数:40,42,44中,“迥异数”为 ;
②计算:f(23)= .
(2)如果一个“迥异数”b的十位数字是k,个位数字是2(k+1),且f(b)=11,请求出“迥异数”b.
(3)如果一个“迥异数”c,满足c5f(c)30,请直接写出满足条件的c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G.求证:
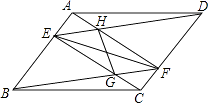
(1)EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有的全等的三角形.
相关试题

