【题目】A、B两地相距300千米,甲、乙两辆汽车同时分别从A、B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(千米)都是行驶时间t(时)的一次函数,图象如图所示,请利用所结合图象回答下列问题: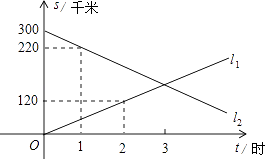
(1)甲的速度为 , 乙的速度为;
(2)求出:l1和l2的关系式;
(3)问经过多长时间两车相遇.
参考答案:
【答案】
(1)60,80
(2)解:根据题意设l1的函数关系式为y=k1t,l2的函数关系式为y=k2t+b,
由图象可知,点(2,120)在l1上,
∴120=2k1,解得k1=60,
∴l1的函数关系式为:y=60t;
由图象可知,点(0,300),(1,220)在l2上,代入有
![]() ,解得
,解得 ![]() ,
,
∴l2的函数关系式为:y=﹣80t+300;
(3)解:设经过x小时后两车相遇,根据题意有
60x+80x=300,解得x= ![]() ,
,
答:经过 ![]() 小时后两车相遇.
小时后两车相遇.
故答案为:(1)60,80.
【解析】(1)由题意可知甲的图像为l1,过(2,120),可求出速度为60km/h,乙的图像上一点(1,220),说明乙1小时行驶(300-220)千米,即80千米;(2)由待定系数法可求出二者的解析式;(3)二者相遇,可根据行程问题,列出方程60x+80x=300;也可根据图像求二直线的交点坐标,即y=60t,y=﹣80t+300联立的方程组求出t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】显示不全在如图所示的平面直角坐标系中有下面各点:A(0,3),B(1,﹣2),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,﹣3),G(4,0).

(1)写出与点C关于坐标轴对称的点;
(2)连接CE,则直线CE与y轴是什么关系(直接写出结论)?
(3)若点P是x轴上的一个动点,连接PD,PF,当PD+PF的值最小时,在图中标出点P的位置,并直接写出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
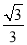 x﹣
x﹣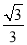 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .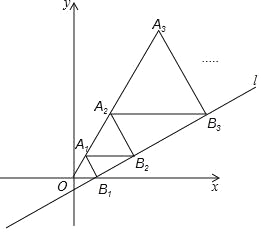
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具经销店在开学时购进了A、B两种型号的计算器,已知:购进A型号的计算器20个,B型号的计算器25个需用1265元;购进A型号的计算器16个,B型号的计算器12个需用748元.求:
(1)A、B两种型号的计算器进价分别是多少元?
(2)在(1)的条件下,若A型号的计算器的售价是30元/个,B型号的计算器的售价是45元/个,商店一次性购进两种型号的计算器各20个,并全部销售,求商店所获利润是多少元?
(3)在两种型号计算器的进价和售价均保持不变的情况下,该商店准备购进A、B两种型号的计算器共40个,且A型号的计算器的数量不得少于5个,问:商店应怎样进货,才能使所获利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且AG=AC,∠ACG=2∠GAF.
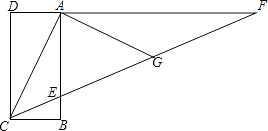
(1)若∠ACB=60°,求∠ECB的度数.
(2)若AF=12cm,AG=6.5cm,求△AEF中EF边上的高? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,善于思考的小军在解方程组
 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5
即2(2x+5y)+y=5③
把方程①代入③得:2×3+y=5
∴y=﹣1
把y=﹣1代入①得x=4
∴方程组的解为
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组
(2)已知x、y满足方程组
①求x2+4y2的值;
②求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2﹣2y=1,那么4x2﹣8y+5= .
相关试题

