【题目】显示不全在如图所示的平面直角坐标系中有下面各点:A(0,3),B(1,﹣2),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,﹣3),G(4,0).
(1)写出与点C关于坐标轴对称的点;
(2)连接CE,则直线CE与y轴是什么关系(直接写出结论)?
(3)若点P是x轴上的一个动点,连接PD,PF,当PD+PF的值最小时,在图中标出点P的位置,并直接写出P点的坐标.
参考答案:
【答案】
(1)解:点C(3,﹣5)关于x轴对称的点E(3,5),点C(3,﹣5)关于y轴对称的点D(﹣3,﹣5);
(2)解:如图所示:直线CE与y轴平行;
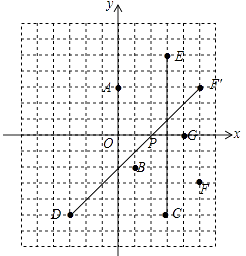
(3)解:作点F关于x轴的对称点F′(5,3),连接DF′交x轴于P,
则DF′的长度即为PD+PF的最小值,
设直线DF′的解析式为:y=kx+b,
∴ ![]() ,
,
∴ ![]() ,
,
∴直线DF′的解析式为:y=x﹣2,
当y=0时,x=2,
∴P点的坐标(2,0).
【解析】(1)关于哪个轴对称,相应坐标不变,另一坐标变为其相反数;(3)动点到两定点距离之和最小问题的解决方法是对称法,作其中一点关于定直线的对称点,连接对称点和另一点,和定直线相交,交点即为最小值位置.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 , 众数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2是一元二次方程x2-2x=3的两个根是,则x1x2的值是( )
A.3B.-3C.2D.-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
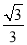 x﹣
x﹣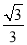 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .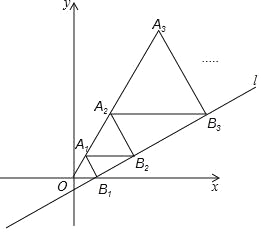
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具经销店在开学时购进了A、B两种型号的计算器,已知:购进A型号的计算器20个,B型号的计算器25个需用1265元;购进A型号的计算器16个,B型号的计算器12个需用748元.求:
(1)A、B两种型号的计算器进价分别是多少元?
(2)在(1)的条件下,若A型号的计算器的售价是30元/个,B型号的计算器的售价是45元/个,商店一次性购进两种型号的计算器各20个,并全部销售,求商店所获利润是多少元?
(3)在两种型号计算器的进价和售价均保持不变的情况下,该商店准备购进A、B两种型号的计算器共40个,且A型号的计算器的数量不得少于5个,问:商店应怎样进货,才能使所获利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距300千米,甲、乙两辆汽车同时分别从A、B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(千米)都是行驶时间t(时)的一次函数,图象如图所示,请利用所结合图象回答下列问题:
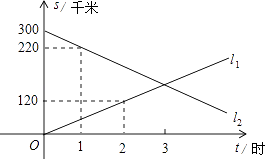
(1)甲的速度为 , 乙的速度为;
(2)求出:l1和l2的关系式;
(3)问经过多长时间两车相遇.
相关试题

